Предмет: Геометрия,
автор: sultan9791
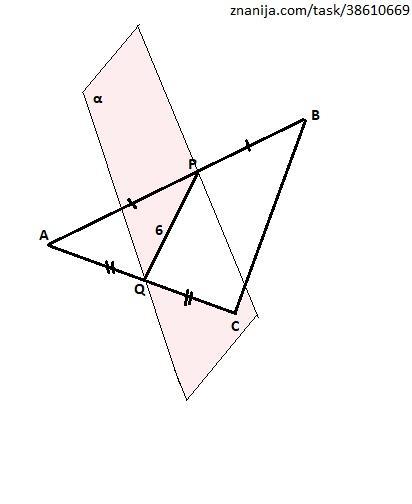
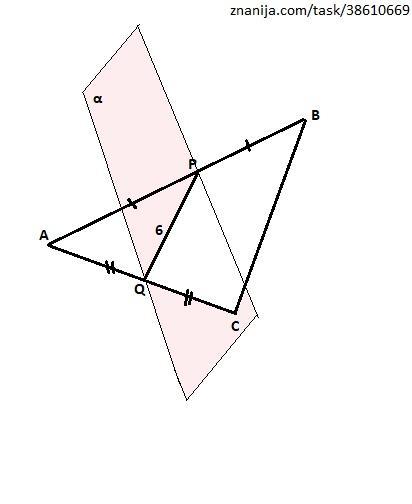
Плоскость α проходит через серединные точки P и Q отрезков AB и AC, соответственно. Если PQ = 6, определи длину средней линии трапеции BPQC.
Ответы
Автор ответа:
1
Ответ:
9 ед.
Объяснение:
Соединим точки Р и Q, В и С. В получившемся треугольнике АВС отрезок PQ является средней линией, так как соединяет середины сторон АВ и АС.
Следовательно, отрезок ВС равен PQ·2 = 12 ед.
Средняя линия трапеции BPQC равна полусумме ее оснований, то есть: (6+12)62 = 9 ед.
P.S. Отметим, что плоскость α в этой задаче совершенно не при чем. Можно было сказать: "даны точки P и Q, являющиеся серединами отрезков АВ и АС соответственно".
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: daniilvolnec
Предмет: Русский язык,
автор: weli675890
Предмет: Українська мова,
автор: vladandriechko4
Предмет: Математика,
автор: koshka453
Предмет: Математика,
автор: lapsik1960