На боковых рёбрах SA и SB пирамиды
SABCD отметили соответственно точки
М и К. Постройте точку пересечения
прямой МК с плоскостью ABC.​

Ответ:

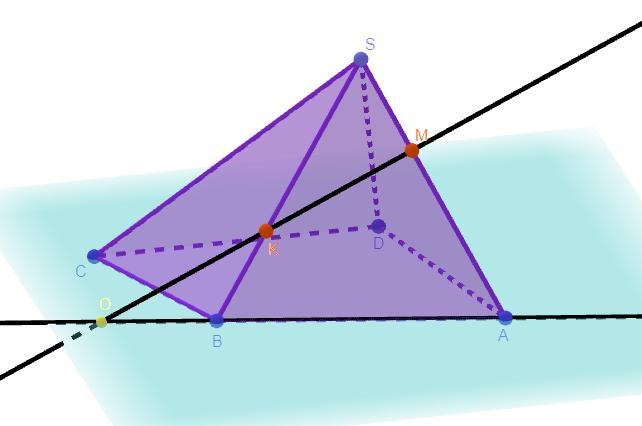
Смотрите рисунок!

Пошаговое объяснение:

Дано: Пирамида SABCD, M ∈ SA, K ∈ SB

Построить: MK ∩ ABC

План построения: Так как по условию M ∈ SA и K ∈ SB, а так как SA ∈ SAB, SB ∈ SAB, то M,K ∈ SAB. По аксиоме стереометрии так как M,K ∈ SAB  прямая MK ∈ SAB. По аксиоме стереометрии так как A,B ∈ SAB прямая, то AB ∈ SAB. Так как MK ∈ SAB и AB ∈ SAB (MK ∦ AB), то MK ∩ AB. Пусть MK ∩ AB = O. Так как AB ∈ ABC и MK ∩ AB = O, то так как O ∈ MK и O ∈  AB, то O ∈ ABC, следовательно точка O является пересечением прямой МК с плоскостью ABC.​