Предмет: Математика, автор: uncolorful

Докажите по индукции данное утверждение, пожалуйста по подробнее

Приложения:

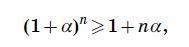
Ответы

Автор ответа: Аноним

Условие не является полным. Это известное неравенство так называемое неравенство Бернулли и оно гласит, что для $\alpha \geq -1$ имеет место неравенство $(1+\alpha)^n\geq 1+n\alpha,~ n \in Z_+$

1) При $n=0$ база индукции выполнено: $1\geq 1$

2) Предположим, что для $n=k$ имеет место неравенство

$(1+\alpha)^k\geq 1+k\alpha$

3) Докажем, что $(1+\alpha)^{k+1}\geq 1+(k+1)\alpha$

$(1+\alpha)^{k+1}=(1+\alpha)(1+\alpha)^k\geq (1+k\alpha)(1+\alpha)= 1+k\alpha+\alpha+k\alpha^2\geq\\ \\ \geq1+k\alpha+\alpha=1+(k+1)\alpha$

Неравенство верно из предположения 2). Утверждение доказано.

uncolorful: в тождественных преобразованиях правой части неравенства я ничего не понял, откуда появились два сомножителя из 1+(k+1)a?

Аноним: вынести за скобки общий множитель альфа

uncolorful: что-то трудно мне даются доказательства в общем виде, не могли бы мне подсказать книжку или ресурс на тему доказательств в подробным описанием методов?

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Английский язык, автор: Nukuma190

составить рассказ , че занимаются русские подростки в свободное время с переводом

2 года назад

Предмет: Українська мова, автор: molenyatko

Утвори слова з частин інших слів . Склади з цими словами речення.

1. Префікс від слова безхмарний , корінь від слова перелісок , закінчення від слова білий?
2. Префікс від слова розмова, корінь від слова махати, закінчення від слова сад ?
3. Префікс від слова розгорнути, корінь від слова садок, закінчення від слова ягідка ?

2 года назад

Предмет: Другие предметы, автор: Аноним

Даю 110 баллов! переведите на французкий!

2 года назад