Предмет: Алгебра, автор: katletta2002

ПОМОГИТЕ ПОЖАЛУЙСТА
СРОЧНО ПЛИЗЗ

Приложения:

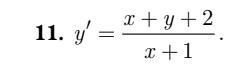
Ответы

Автор ответа: GluV

Ответ:

$y=(x+1)*(ln(x+1)-\frac{1}{x+1}+Const)$

Объяснение:

Перепишем уравнение в виде

$y'*(x+1)-y=(x+2)$

На первом шаге найдем решение уравнения

$y'*(x+1)-y=0$

$\frac{y'}{y} =\frac{1}{(x+1)}$

$y=C*(x+1)$

Будем искать общее решение, как $f(x)*(x+1)$

Подставляем в первое уравнение и получаем

$f'(x)*(x+1)^{2} =x+2$

$f'(x)=\frac{x+2}{(x+1)^{2}}=\frac{1}{(x+1)} +\frac{1}{(x+1)^{2}}$

Интегрируем левую и правую часть и получаем

$f(x)=ln(x+1)-\frac{1}{x+1} +C$

Тогда общее решение будет

$y=(x+1)*(ln(x+1)-\frac{1}{x+1}+Const)$

Проверяем себя в программе Maxima

Приложения:

Интересные вопросы

Предмет: Другие предметы, автор: Musagitovailmi

2 года назад

Предмет: Русский язык, автор: andreevav201162

2 года назад

Предмет: Русский язык, автор: Klaproth

2 года назад

Предмет: Геометрия, автор: антончик1

8 лет назад

Предмет: Математика, автор: ТрезвыйГолубь

8 лет назад