Предмет: Алгебра, автор: Dzajranibragimova06

Помогите пожалуйста!
sin x+cos x=1

Ответы

Автор ответа: Аноним

Ответ:

$\displaystyle \left [{{x = 2\pi n} \atop {x=н (\pi + 4\pi n)}} \right. \, , n\in\mathbb{Z}$

Объяснение:

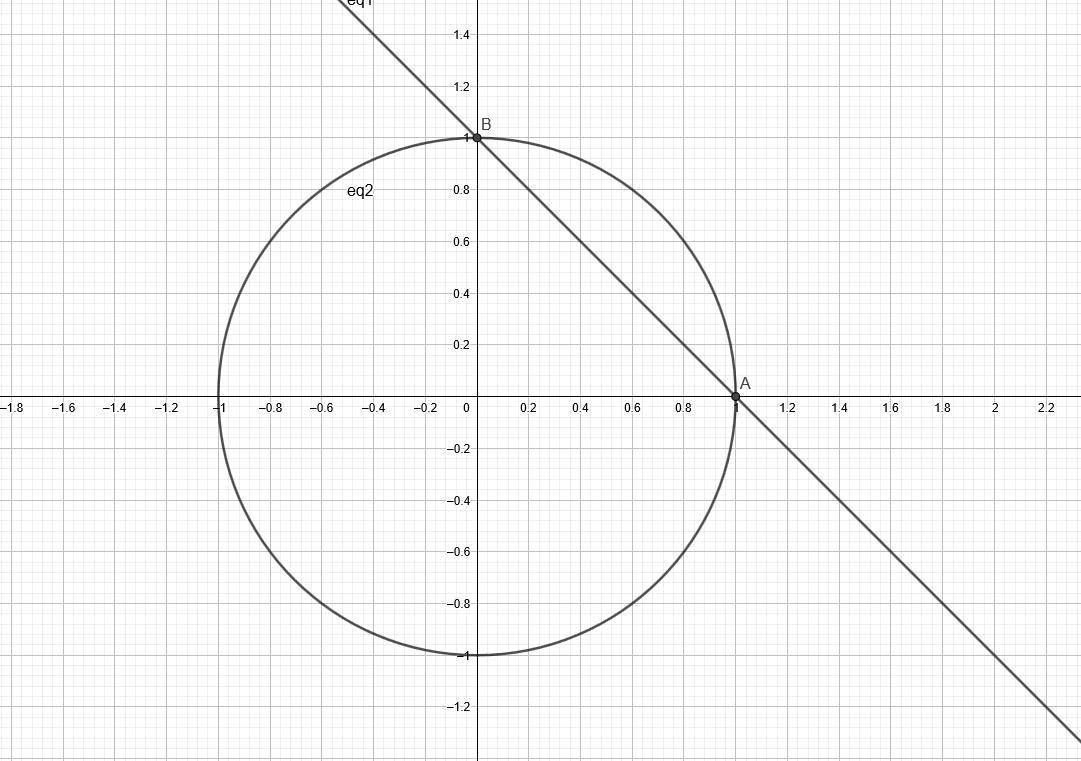
Решу графически:

Пусть sin x = u и cos x = v

Тогда уравнение имеет вид u + v = 1

Но по ОТТ $u^2+v^2=1$

Тогда построим график системы

$\displaystyle \Gamma_{u(v)}=\left \{ {{u+v=1} \atop {u^2+v^2=1}} \right.$

График второго уравнения - окружность с центром в точке (0 0) и радиусом 1.

График первого - прямая, проходящая через точки (0 1) и (1 0) (см. рисунок)

Тогда пересечения этих двух графиков - точки А и В - в полярных координатах - $2\pi n$ и $н(\pi+4\pi n)$ , где $n\in\mathbb{Z}$

Приложения:

Автор ответа: Universalka

$Sinx+Cosx=1\\\\\sqrt{2}(\frac{1}{\sqrt{2}}Sinx+\frac{1}{\sqrt{2}}Cosx)=1\\\\\sqrt{2}(SinxCos\frac{\pi }{4} +CosxSin\frac{\pi }{4} )=1\\\\\sqrt{2}Sin(x+\frac{\pi }{4})=1\\\\Sin(x+\frac{\pi }{4} )=\frac{\sqrt{2}}{2}$

$\left[\begin{array}{ccc}x+\frac{\pi }{4}=\frac{\pi }{4}+2\pi n,n\in Z\\x+\frac{\pi }{4}=\pi-\frac{\pi }{4}+2\pi n,n\in Z\end{array}\right\\\\\left[\begin{array}{ccc}x=2\pi n,n\in Z \\x=\frac{\pi }{2}+2\pi n,n\in Z\end{array}\right$