помогите пожалуйста
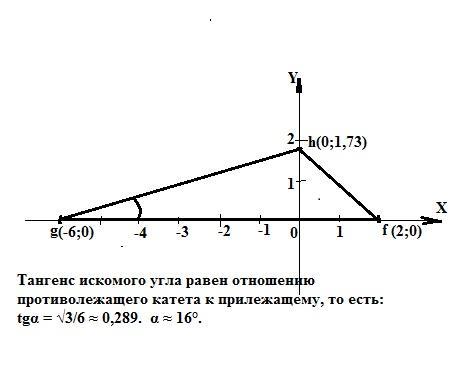
найдите угол FGH треугольника,если f(2;0),g(-6;0), h(0;√3)​

Ответ:

∠FGH = arccos0,9608 ≈ 16°.

Объяснение:

Угол между векторами  a, b и c определяется по формуле:

cosα=(Xa·Xb+Ya·Yb)/[√(Xa²+Ya²)·√(Xb²+Yb²)].

В нашем случае надо определить угол между векторами GF и GH.

Найдем координаты этих векторов и их модули:

Вектор GF{Xf - Xg;Yf-Yg} = GF{2-(-6);0-0} =GF{8;0}.

|GF| = √(8²+0²) = 8.

Вектор GH{Xh - Xg;Yh-Yg} = GH{0-(-6);√3-0} =GF{6;√3}.

|GF| = √(36+3) = √39.

Тогда

cos(FGH) = (8·6 + 0·√3)/(8·√39) = 48/(8·√39) = 6√39/39 ≈ 0,9608.

∠FGH = arccos0,9608 ≈ 16° (по калькулятору).

Или так:

По рисунку на координатной плоскости тангенс искомого угла FGH равен отношению противолежащего катета "h" к прилежащему "g", то есть:

tgα = √3/6 ≈ 0,289.  α ≈ arctg0,269 ≈ 16° (по калькулятору).