Предмет: Алгебра, автор: konstantsya

Решить показательное неравенство без замены!

Приложения:

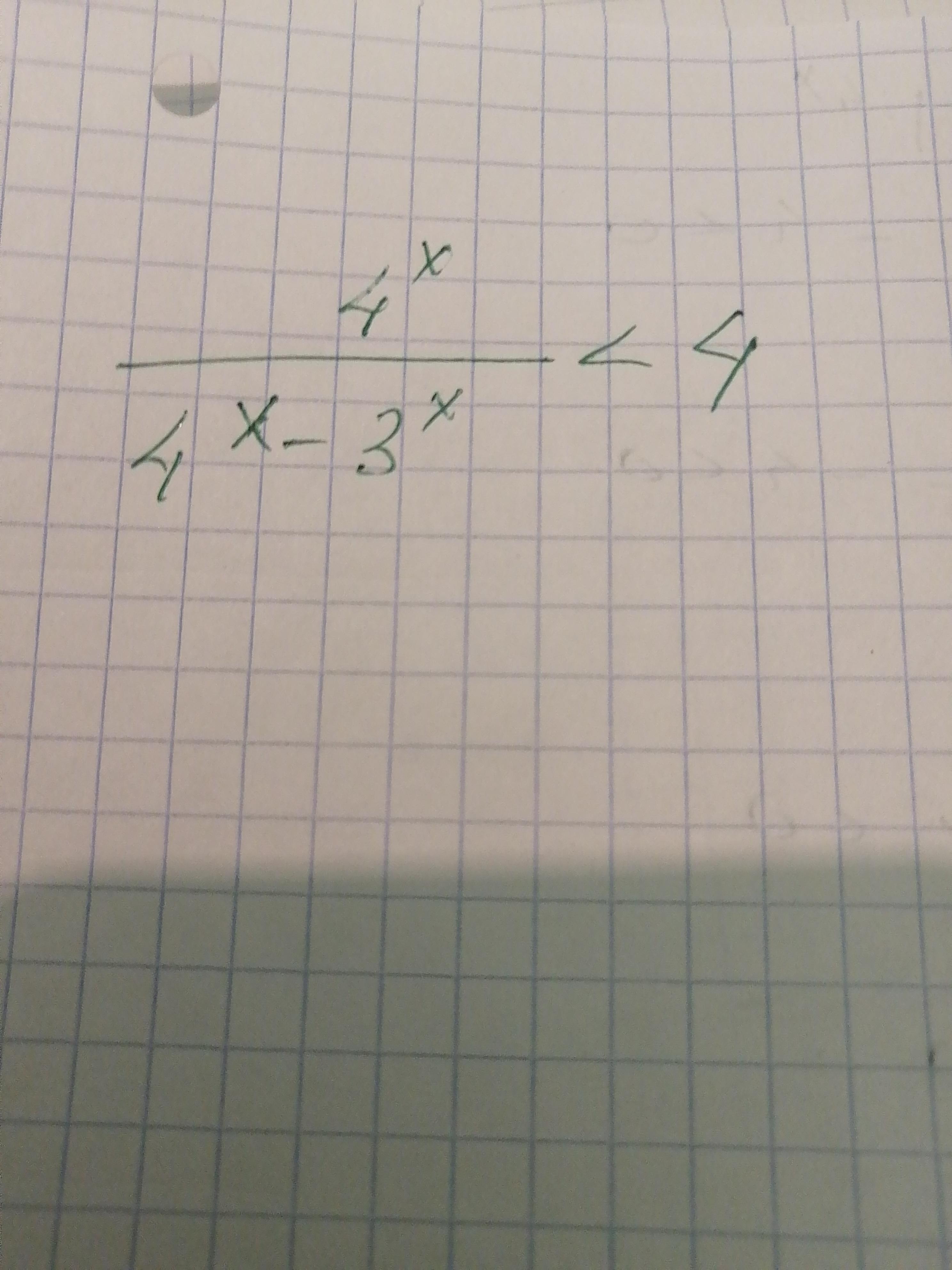
Ответы

Автор ответа: Artem112

$\dfrac{4^x}{4^x-3^x} <4$

Перенесем все слагаемые в левую часть:

$\dfrac{4^x}{4^x-3^x} -4<0$

Приведем к общему знаменателю:

$\dfrac{4^x}{4^x-3^x} -\dfrac{4(4^x-3^x)}{4^x-3^x} <0$

Выполним вычитание:

$\dfrac{4^x-4(4^x-3^x)}{4^x-3^x} <0$

$\dfrac{4^x-4\cdot4^x+4\cdot3^x}{4^x-3^x} <0$

$\dfrac{4\cdot3^x-3\cdot4^x}{4^x-3^x} <0$

Разделим числитель и знаменатель дроби на $3^x\neq 0$ :

$\dfrac{\dfrac{4\cdot3^x}{3^x} -\dfrac{3\cdot4^x}{3^x} }{\dfrac{4^x}{3^x} -\dfrac{3^x}{3^x} } <0$

$\dfrac{4-3\cdot\left(\dfrac{4}{3}\right)^x }{\left(\dfrac{4}{3}\right)^x -1 } <0$

Также удобно обе части неравенства разделить на 3:

$\dfrac{\dfrac{4}{3} -\left(\dfrac{4}{3}\right)^x }{\left(\dfrac{4}{3}\right)^x -1 } <0$

Перепишем неравенство в виде:

$\dfrac{\left(\dfrac{4}{3}\right)^x-\dfrac{4}{3} }{\left(\dfrac{4}{3}\right)^x -1 } >0$

Нули числителя и знаменателя определяются выражениями:

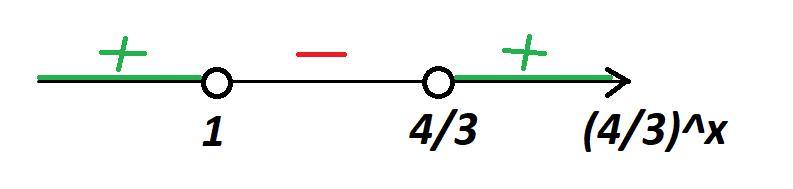
$\left(\dfrac{4}{3}\right)^x=\dfrac{4}{3};\ \left(\dfrac{4}{3}\right)^x=1$

Решая неравенство методом интервалов относительно $\left(\dfrac{4}{3}\right)^x$ , получим:

$\left[\begin{array}{l} \left(\dfrac{4}{3}\right)^x<1\\ \left(\dfrac{4}{3}\right)^x>\dfrac{4}{3} \end{array}$

Далее получим:

$\left[\begin{array}{l} \left(\dfrac{4}{3}\right)^x<\left(\dfrac{4}{3}\right)^0\\ \left(\dfrac{4}{3}\right)^x>\left(\dfrac{4}{3}\right)^1 \end{array}$

$\left[\begin{array}{l} x<0\\ x>1 \end{array}$

$x\in(-\infty;\ 0)\cup(1;\ +\infty)$

Можно было преобразовать неравенство к следующему виду:

$\dfrac{\left(\dfrac{4}{3}\right)^x-\left(\dfrac{4}{3}\right)^1 }{\left(\dfrac{4}{3}\right)^x -\left(\dfrac{4}{3}\right)^0 } >0$

Так как функция $y=\left(\dfrac{4}{3}\right)^x$ возрастает на всей области определения, то можно сразу перейти к более простому неравенству, заменяя разности значений функции соответствующими разностями значений аргументов: