(100б) Найдите область значений функции y=(4x-12)/x^2

Объяснение:

Дана функция:

Найти: Е(у)

Рассмотрим данную функцию:

ОДЗ: х≠0 ⇒ D(y)=(-∞;0)∪(0;+∞)

⇒ ось 0у график не пересекает.

Изобразим схематично данную функцию.

При х<0, y<0, то есть слева от оси 0у значения у отрицательны.

Рассмотрим правую часть функции:

График пересекает ось 0х в точке

4х-12=0

х=3

То есть до 0<х<3, y<0. При х>3, у>0.

Найдем экстремумы функции. Для этого найдем производную:

y'=0 ⇒ х=6

Имеем две точки:

х=6;   х≠0

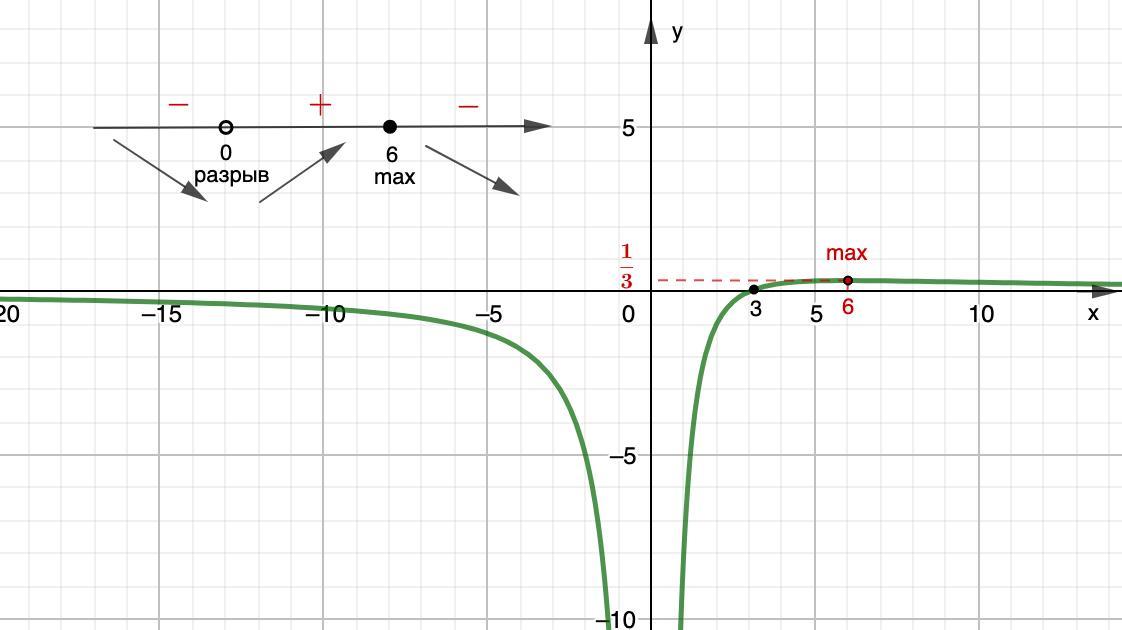
Отметим их на числовой оси (см. рис)

Видим, что при х∈(-∞;0)∪[6;+∞) функция убывает;

а при х∈(0;6] функция возрастает.

х=6 - точка max.

Изобразим график.

Найдем

⇒