Предмет: Алгебра, автор: Аноним

помогите пожалуйста

Приложения:

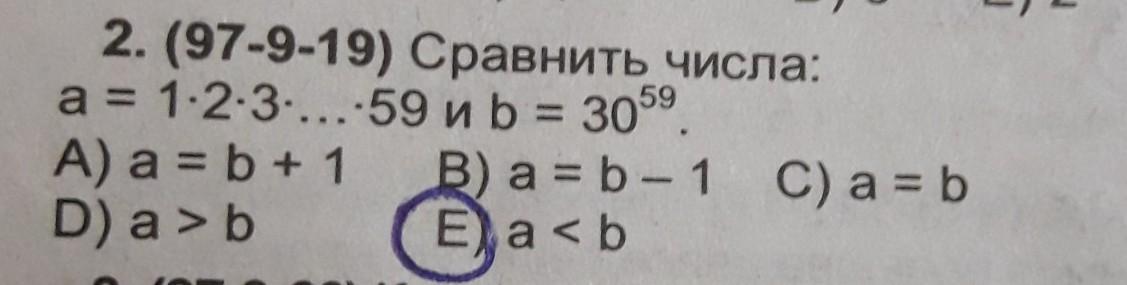
Ответы

Автор ответа: yugolovin

Те, кто изучал высшую математику, точнее, изучал формулу Стирлинга, сразу выберут правильный ответ: конечно, a<b. Вопрос в том, как доказать это школьными методами. Совсем простого способа я не увидел, но надежда есть. Кстати, вместо произведения натуральных чисел от 1 до n люди давно придумали короткое обозначение n! (n-факториал), есть также понятие "двойной факториал" - это произведение натуральных чисел через одно; например,

$6!!=6\cdot 4\cdot 2;\ 5!!=5\cdot 3\cdot 1$ ;

"тройной факториал"; например,

$9!!!=9\cdot 6\cdot 3;\ 8!!! =8\cdot 5\cdot 2; 7!!!=7\cdot 4\cdot 1;$

и так далее.

Будем упрощать доказываемое неравенство a<b, увеличивая a и сокращая на получаемые общие множители.

$a=59!<2\cdot 4\cdot 4\cdot 6\cdot 6\ldots 58\cdot 58\cdot 60=\frac{(60!!)^2}{120}=\frac{(2^{30}\cdot 30!)^2}{120}=\frac{2^{59}\cdot (30!)^2}{60}.$

Получившееся число мы сравниваем с $30^{59}.$ Разделив оба на $2^{59},$ получаем для сравнения числа $c=(30!)^2$ и $d=60\cdot 15^{59}=4\cdot 15^{60}.$

Извлечем квадратный корень из этих чисел, получив для сравнения числа $f=30!$ и $g=2\cdot 15^{30}.$

$f<3\cdot 3\cdot 3\cdot 6\cdot 6\cdot 6\cdot 9\ldots \cdot 30=(30!!!)^3=(3^{10}\cdot 10!)^3=3^{30}\cdot (10!)^3.$

Сократив получившееся число и g на 3 в 30-й степени, получаем для сравнения числа $m=(10!)^3$ и $n=2\cdot 5^{30}.$

Чтобы легче было извлечь корень третьей степени, уменьшим n в два раза, после чего этот корень извлечем из обоих чисел. Получаем для сравнения числа $p=10!$ и $q=5^{10}.$

Эти числа можно уже непосредственно вычислить, либо снова продолжить оценки, хотя с осторожностью, поскольку эти числа уже не слишком отличаются друг от друга.

Например, так: $p=2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7\cdot 8\cdot 9\cdot 10=(2\cdot 7)\cdot (3\cdot 8)\cdot (4\cdot 6)\cdot 5\cdot 9 \cdot 2\cdot 5=$