Предмет: Геометрия,
автор: MilyaMashelikov
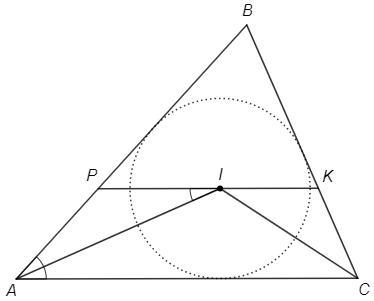
через центр вписанной в треугольник АБС окружности проведена прямая РК, параллельная стороне АС (Р принадлежит АБ, К принадлежит БС). Докажите, что РК = АР+КС
Ответы
Автор ответа:
9
Центр вписанной окружности (I) - точка пересечения биссектрис.
AI - биссектриса, PAI=CAI
PIA=CAI (накрест лежащие при PK||AC)
PAI=PIA => △API - равнобедренный, PA=PI
Аналогично KC=KI
PK =PI+KI =PA+KC
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: Giharka83
Предмет: Русский язык,
автор: vovanloginov679
Предмет: Русский язык,
автор: talealiev
Предмет: Математика,
автор: 375333919473
Предмет: Математика,
автор: Мария46990