Предмет: Алгебра,
автор: Trane2055
Решите пожалуйста уравнение в 3 под буквой а)
Приложения:
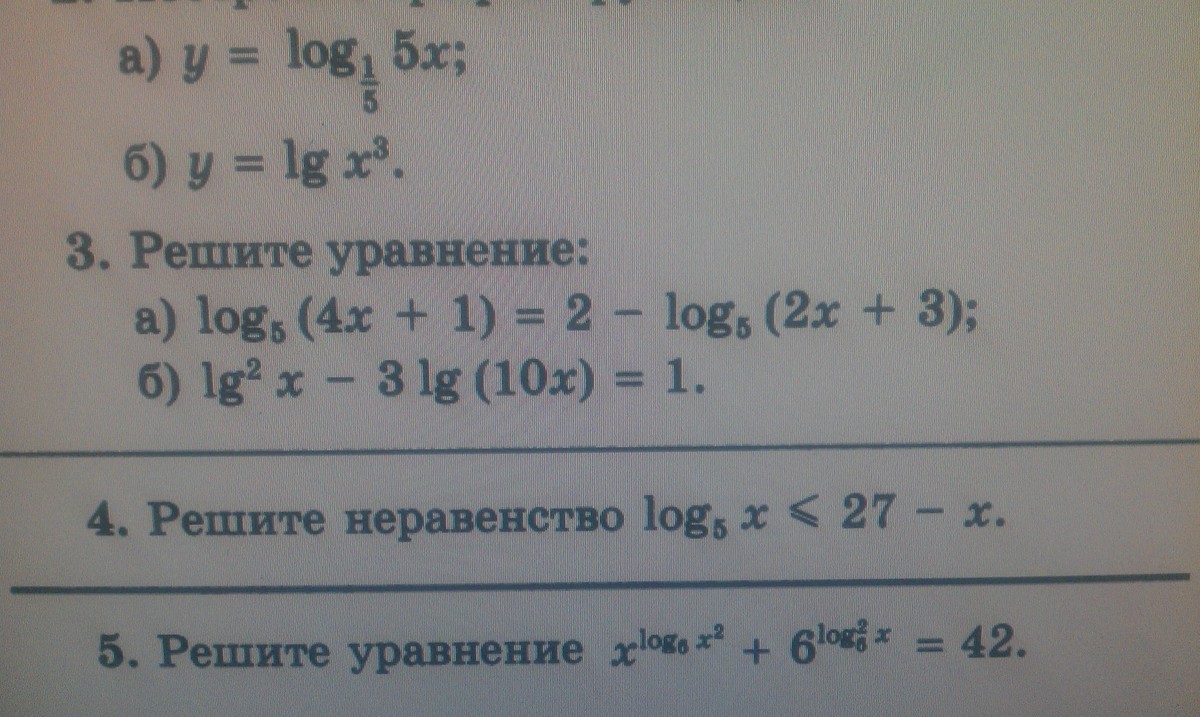
Ответы
Автор ответа:
0
log5(4x + 1) = 2 - log5(2x + 3)
log5(4x + 1) + log5(2x + 3) = log5(25)
log5((4x + 1)(2x + 3)) = log5(25)
(4x + 1)(2x + 3) = 25
8x^2 + 12x + 2x + 3 - 25 = 0
8x^2 + 14x - 22 = 0
4x^2 + 7x - 11 = 0
D = 49 + 4*11*4 = 225
x1 = (-7 + 15)/8 = 8/8 = 1
x2 = (-7 - 15)/8 = -22/8 = -2.75
Проверка корней:
x = 1, log5(4 + 1) = 2 - log5(2 + 3) - верно
x = -2.75, log5(4*(-2,75) + 1) = 2 - log5(2*(-2,75) + 3) - не верно, т.к. подлогарифмические выражения отрицательные.
Ответ: x = 1
log5(4x + 1) + log5(2x + 3) = log5(25)
log5((4x + 1)(2x + 3)) = log5(25)
(4x + 1)(2x + 3) = 25
8x^2 + 12x + 2x + 3 - 25 = 0
8x^2 + 14x - 22 = 0
4x^2 + 7x - 11 = 0
D = 49 + 4*11*4 = 225
x1 = (-7 + 15)/8 = 8/8 = 1
x2 = (-7 - 15)/8 = -22/8 = -2.75
Проверка корней:
x = 1, log5(4 + 1) = 2 - log5(2 + 3) - верно
x = -2.75, log5(4*(-2,75) + 1) = 2 - log5(2*(-2,75) + 3) - не верно, т.к. подлогарифмические выражения отрицательные.
Ответ: x = 1
Автор ответа:
0
а какое тут ОДЗ?
Автор ответа:
0
у меня тоже одз (0.25 до плюс бесконечности) получилось,а разве логарифм может принимать отрицательные значения входящие в это одз?
Автор ответа:
0
ОДЗ от МИНУС 0.25. А логарифм сам может быть отрицательным, например log5(1/5) = -1
Интересные вопросы
Предмет: Алгебра,
автор: Aruzhan0064
Предмет: Алгебра,
автор: dsfsh
Предмет: Математика,
автор: kozacokdpra
Предмет: Геометрия,
автор: lys
Предмет: Биология,
автор: DiAnA2712