Предмет: Геометрия, автор: mlioubakova

трапеция ABCD расположена в плоскости альфа. Диагонали трапеции параллельны плоскости альфа. Через вершины А и В проведены параллельные прямые, которые пересекают плоскость альфа в точках E и F. Докажите, что EABF параллелограмм.

Ответы

Автор ответа: KuOV

В задаче неправильное условие.
Должно быть:
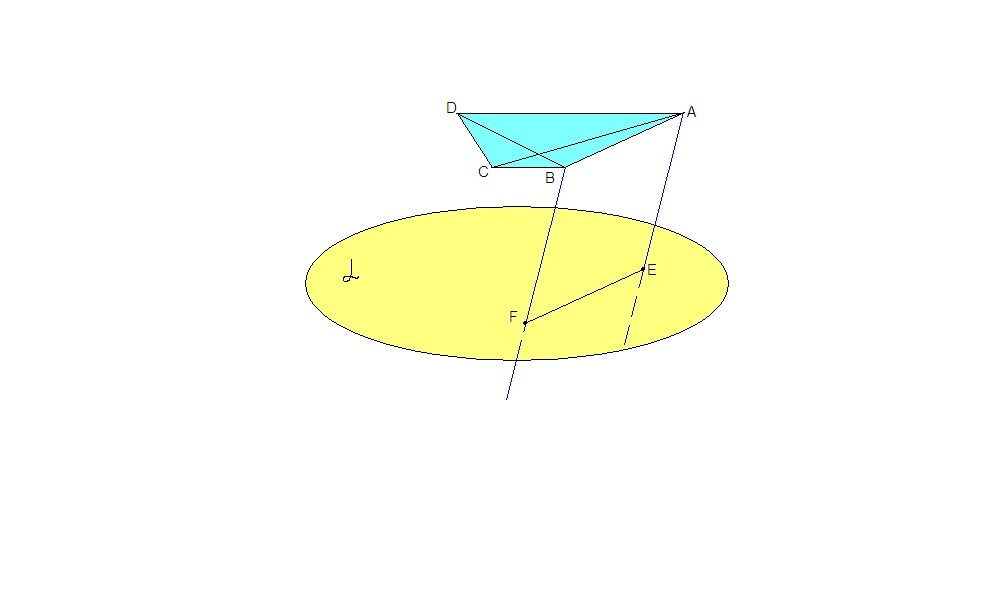
Трапеция ABCD (AD и ВС - основания) расположена вне плоскости α. Диагонали трапеции параллельны плоскости .
Через вершины А и В проведены параллельные прямые, которые пересекают плоскость α в точках E и F. Докажите, что EABF параллелограмм.

Если диагонали трапеции параллельны плоскости α, то и плоскость трапеции параллельна плоскости α: диагонали - две пересекающиеся прямые плоскости трапеции, а в плоскости α найдутся две прямые, параллельные им.

Значит АВ║α.

Параллельные прямые AE и BF задают плоскость, которая проходит через АВ, параллельную α, и пересекает α. Значит линия пересечения - EF - параллельна АВ..

В четырехугольнике противолежащие стороны параллельны, значит это - параллелограмм.

Приложения: