Предмет: Алгебра, автор: CatherineAfanasova

срочно надо решить логарифмическое уравнение

$log_{4} (x-2)^{2} +log_{2}(1-x)=log_{2}(3) +1$

Ответы

Автор ответа: tushkanchik335

Ответ:

-1

Объяснение:

решение в прикрепленном файле, удачи)

Приложения:

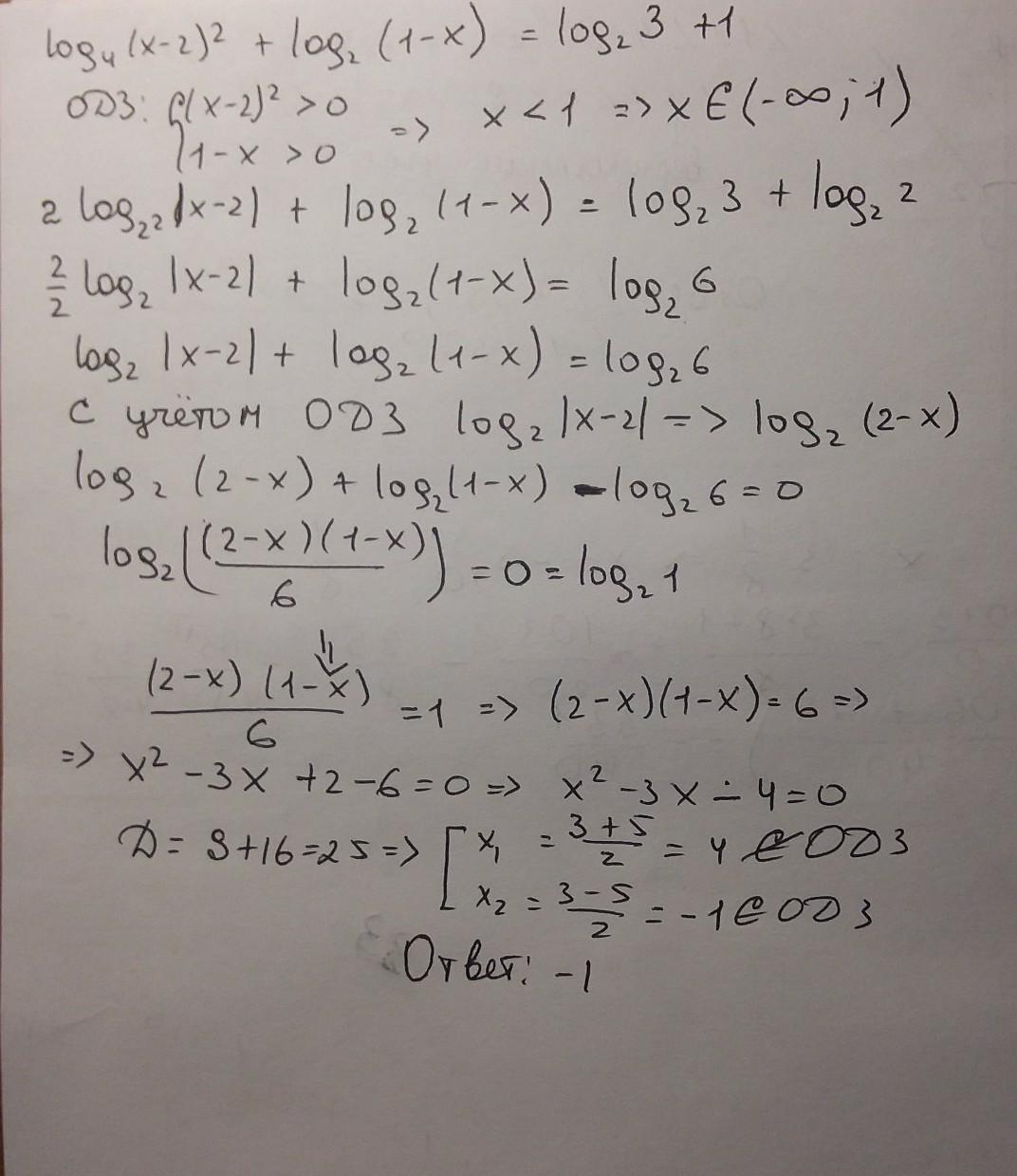
Автор ответа: Kean1234

Ответ:

x = -1

Объяснение:

$log_{4} (x-2)^2 + log_{2}(1-x) = log_{2} (3) + 1;$

ОДЗ: (1 - x) > 0 ⇒ x < 1

$log_{4} (x-2)^2 = log_{2^2} (x-2)^2$

$log_aX + log_aY = log_a(XY)$ - логарифм произведения двух положительных чисел

$log_{a^k}X^n = \frac{n}{k} log_aX$ - логарифм степени числа

$log_{2^2}(x-2)^2 + log_2(1-x) = \frac{2}{2}log_2(|x-2|) + log_2(1-x) = log_2(|x-2|) + log_2(1-x) = log_2((|x-2|)(1-x))$

$1 = log_22$

$log_23 + log_22 = log_26$

$log_2((|x-2|)(1-x)) = log_26$

Избавимся от логарифма и модуля выражения

1) При x - 2 ≥ 0 - вариант не подходит по ОДЗ (x < 1)

2) При x - 2 < 0

$(2-x)(1-x) = 6\\2 - 2x - x + x^2 = 6\\x^2 - 3x - 4 = 0$

$x1 = \frac{3 - 5}{2} = -1\\\\x2= \frac{3 + 5}{2} = 4\\$

x2 - посторонний корень, не подходит по ОДЗ

Ответ: x = -1

Интересные вопросы

Предмет: Математика, автор: dada2013dada1

2 года назад

Предмет: Математика, автор: NatashaDimidova

2 года назад

Предмет: Математика, автор: okb070882

2 года назад

Предмет: Биология, автор: Flamster

8 лет назад

Предмет: Математика, автор: anaumova21

8 лет назад