Предмет: Математика,
автор: xzzzzzzzz35
На рисунке ∠MKL = ∠NLK, ∠NKL = ∠MLK. Докажи, что треугольники KOM и LON равны.

Следовательно, по второму признаку равенства треугольников,
так как KL – общая сторона и по условию задачи
к этой стороне прилегают равные углы.
KM = LN, ∠M = ∠N.
Если ∠MKO = ∠MKL – ∠NKL, ∠NLO = ∠NLK – ∠MLK,
Тогда из равенства треугольников KML и LNK следует, что
равных углов равны.
поставьте в правильную
последовательность
Приложения:

malinkaza:
у меня лимит люди спасайте
(((
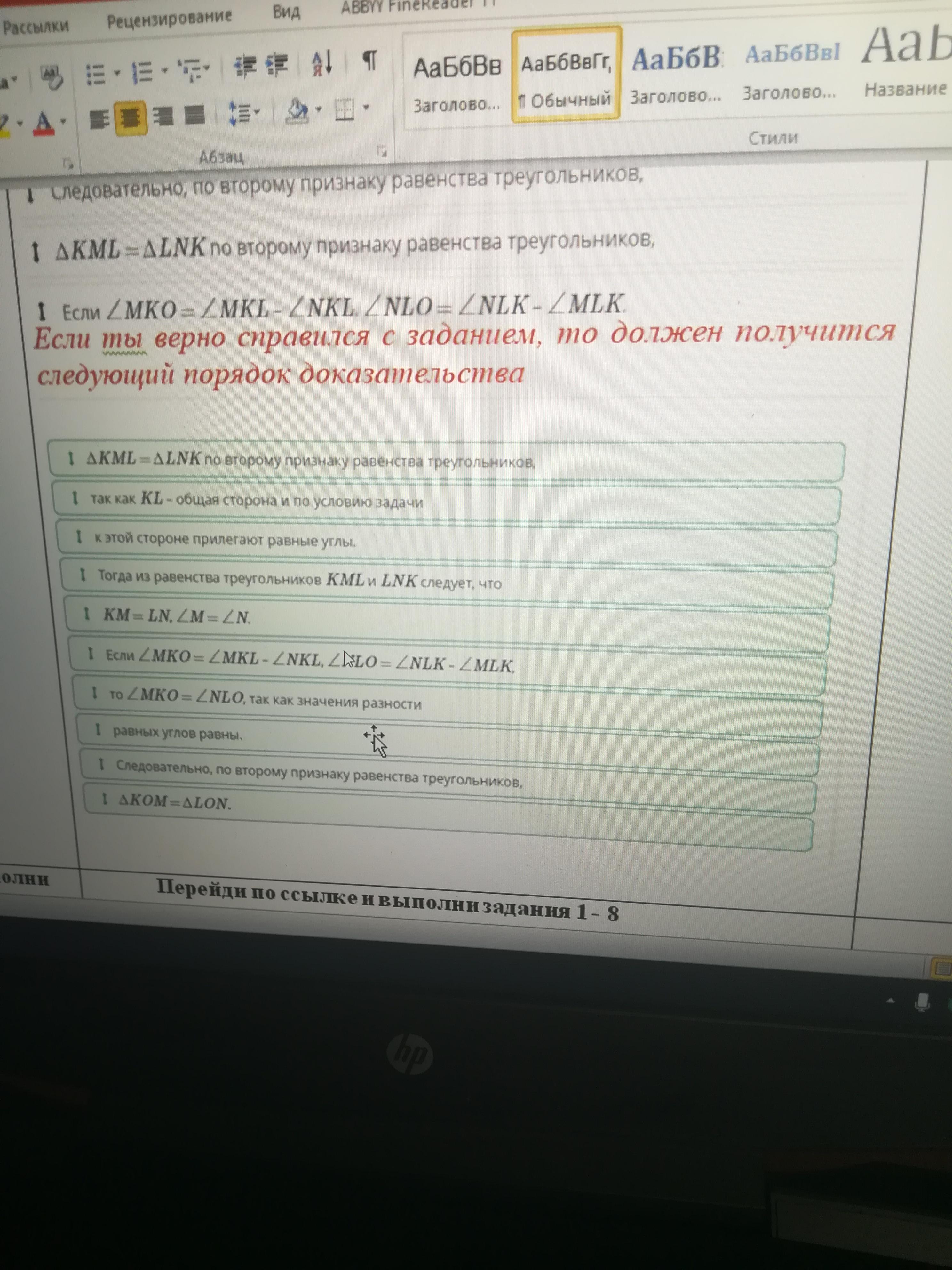
∆KML = ∆LNK по второму признаку равенства треугольников,
так как KL – общая сторона и по условию задачи
к этой стороне прилегают равные углы.
Тогда из равенства треугольников KML и LNK следует, что
KM = LN, ∠M = ∠N.
Если ∠MKO = ∠MKL – ∠NKL, ∠NLO = ∠NLK – ∠MLK,
то ∠MKO = ∠NLO, так как значения разности
равных углов равны.
Следовательно, по второму признаку равенства треугольников,
∆KOM = ∆LON.
так как KL – общая сторона и по условию задачи
к этой стороне прилегают равные углы.
Тогда из равенства треугольников KML и LNK следует, что
KM = LN, ∠M = ∠N.
Если ∠MKO = ∠MKL – ∠NKL, ∠NLO = ∠NLK – ∠MLK,
то ∠MKO = ∠NLO, так как значения разности
равных углов равны.
Следовательно, по второму признаку равенства треугольников,
∆KOM = ∆LON.
Ответы
Автор ответа:
141
Ответ: все на фото
Пошаговое объяснение: пж 5 звезд
Приложения:
пж
паж
малю
∆KML = ∆LNK по второму признаку равенства треугольников,
так как KL – общая сторона и по условию задачи
к этой стороне прилегают равные углы.
Тогда из равенства треугольников KML и LNK следует, что
KM = LN, ∠M = ∠N.
Если ∠MKO = ∠MKL – ∠NKL, ∠NLO = ∠NLK – ∠MLK,
то ∠MKO = ∠NLO, так как значения разности
равных углов равны.
Следовательно, по второму признаку равенства треугольников,
∆KOM = ∆LON.
так как KL – общая сторона и по условию задачи
к этой стороне прилегают равные углы.
Тогда из равенства треугольников KML и LNK следует, что
KM = LN, ∠M = ∠N.
Если ∠MKO = ∠MKL – ∠NKL, ∠NLO = ∠NLK – ∠MLK,
то ∠MKO = ∠NLO, так как значения разности
равных углов равны.
Следовательно, по второму признаку равенства треугольников,
∆KOM = ∆LON.
Қазақша бар ма?
спасибо правильно !
все правильно
спасибо
Интересные вопросы
Предмет: Українська мова,
автор: balakina02
Предмет: Геометрия,
автор: мегаботан555
Предмет: Литература,
автор: matsicgame
Предмет: Информатика,
автор: STRELOID