Предмет: Математика, автор: gaptova04a

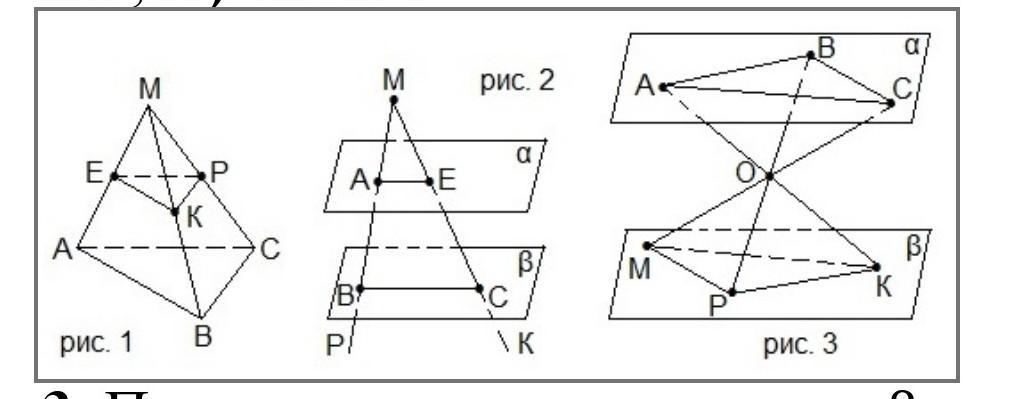
На рисунке 1 точки: Е-середина АМ, К-середина ВМ, Р-середина СМ. Площадь треугольника ЕКР равна 24 см2.

Найти площадь треугольника АВС.

A) 96 см2; B) 64 см2; C) 72 см2; D) 48 см2.

Приложения:

Ответы

Автор ответа: mathkot

Ответ:

$S_{ABC} = 96$ сантиметров квадратных

Пошаговое объяснение:

Дано: MABC - тетраэдр, EM = EA, MK = BK, MP = PC. $S_{EKP} = 24$ сантиметров квадратных.

Найти: $S_{ABC} - ?$

Решение: Так как по условию EM = EA, MK = BK, MP = PC , то MA = 2ME = 2EA, MB = 2MK = BK, MC = 2MP = 2PC, следовательно $\frac{ME}{MA} = \frac{ME}{2ME} = 0,5$ , $\frac{MK}{MB} = \frac{MK}{2MK} = 0,5$ , $\frac{MP}{MC} = \frac{MP}{2MP} = 0,5$ .Тогда $\frac{ME}{MA} = \frac{MK}{MB} = \frac{MP}{MC}$ . Тогда $\overrightarrow{MA} = k\overrightarrow{ME} , \overrightarrow{MB} = k\overrightarrow{MK}, \overrightarrow{MC} = k\overrightarrow{MP}$ где $k > 0.$ $k = \frac{\overrightarrow{MA}}{\overrightarrow{ME}} = \frac{\overrightarrow{2ME}}{\overrightarrow{ME}} = 2$ . Тогда треугольник ΔEPK гомотетичный треугольнику ΔABC. Тогда по свойствам гомотетии: $\frac{S_{ABC}}{S_{EKP}} = k^{2} \Longrightarrow {S_{ABC} = k^{2} *S_{EKP} = 2^{2} * 24 = 4 * 24 = 96$ сантиметров квадратных.