Предмет: Геометрия,
автор: alinavolk8025
SOOOOOOOS
Концы двух равных пересекающихся отрезков АС и BD лежат на двух параллельных плоскостях.
А) при каком дополнительном условии пересечения отрезков ABCD-прямоугольник?
В) докажите, что если АBCD не является прямоугольником, то ABCD - равнобоковая трапеция
Ответы
Автор ответа:
4
Ответ:
А) АС и BD - равные диагонали четырехугольника ABCD.
Чтобы ABCD был прямоугольником, необходимо, чтобы диагонали точкой пересечения делились пополам, т.е.
АО = ОС и ВО = OD.
В) Если параллельные плоскости пересечены третьей плоскостью, то линии пересечения параллельны.
Плоскости α и β параллельны и пересечены третьей плоскостью (АВС) по прямым AB и CD, значит AB ║ CD.
Так как ABCD не является прямоугольником, то AD ∦ BC (иначе четырехугольник был бы параллелограммом с равными диагоналями, т.е. прямоугольником).
Итак, две стороны четырехугольника ABCD параллельны, а две другие - не параллельны, значит это трапеция.
Если в трапеции диагонали равны, то она равнобедренная.
Приложения:
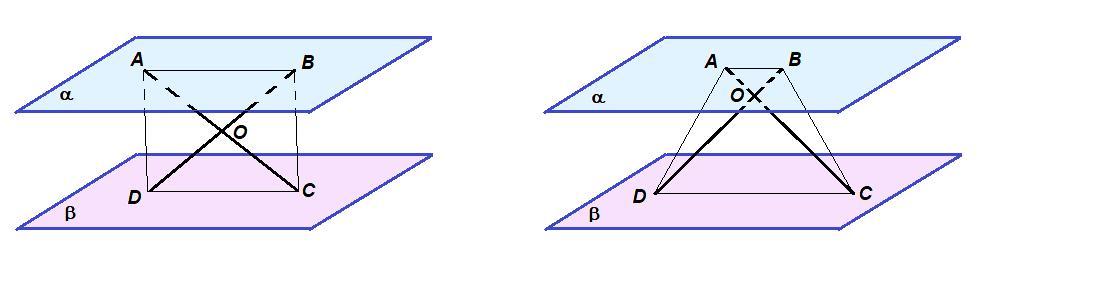
Интересные вопросы
Предмет: Математика,
автор: serega5132
Предмет: Математика,
автор: danis3352
Предмет: Русский язык,
автор: kombsveta56
Предмет: Экономика,
автор: Voloda98
Предмет: МХК,
автор: Otlihnik666