Помогите пожалуйста.
В круге проведена хорда длиной 32 дм, которая находится на расстоянии 12 дм от центра круга.

Длина окружности равна ... дм;
π =3,14.

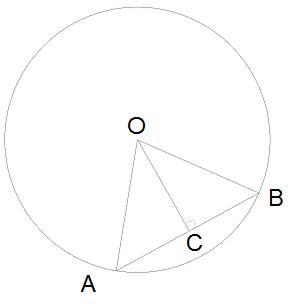
Дано:

Окружность (O;R)

ΔAOB - равнобедренный

AB = 32 дм

OC = 12 дм

-------------------------------------------

Найти:

C - ?

Решение:

1) Рассмотрим ΔAOB :

   ОА=ОВ=R                        } ⇒ ΔAOB - равнобедренный,

   ОС - высота и медиана }

значит: AC = CB = AB/2 = 32 дм/2 = 16 дм

2) ΔOCB — прямоугольный, так как ∠BCO = 90°, следовательно мы пользуемся по по теореме Пифагора:

BO = √(OC² + CB²) = √((12 дм)² + (16 дм)²) = √(144 дм² + 256 дм²) = √(400 дм²) = 20 дм ⇒ R = BO = 20 дм

3) Воспользуемся формулой длины окружности, именно по такой формуле мы найдем длину окружности: C = 2πR

C = 2π × 20 дм = 40π дм = 40×3,14 дм = 125,6 дм

Ответ: C = 125,6 дм

Решено от :