Здравствуйте, срочно нужно.

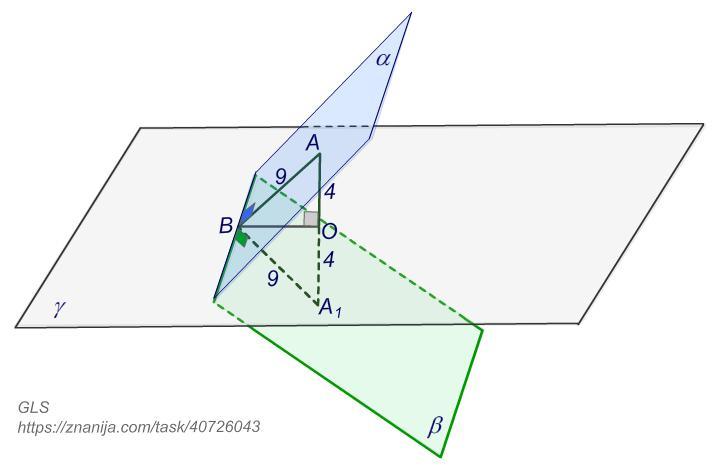
Грани α и β двугранного угла симметричны относительно плоскости симметрии γ. Известно, что точка находится в плоскости α на расстоянии 9 от ребра двугранного угла и на расстоянии 4 от плоскости симметрии γ.

1) Определи косинус двугранного угла ∡ϕ.
(В ответ введи несократимую дробь, для знака ответа — отдельное поле, в которое введи знак только для отрицательных ответов.)

ϕ=

Определи вид двугранного угла:
острый
тупой
прямой

Ответ:

Двугранный угол острый.

Объяснение:

• Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости γ - это зеркальная симметрия пространства относительно плоскости γ.
• Плоскость γ является плоскостью симметрии.

Точка A₁ является образом точки A при зеркальной симметрии относительно плоскости γ.  

Это значит, что отрезок AA₁ перпендикулярен плоскости γ и делится ею пополам.

AO = OA₁ = 4, где точка O - точка пересечения отрезка AA₁ с плоскостью γ.

Тогда AA₁ = 4 · 2 = 8.

• Расстоянием от точки до прямой является длина перпендикуляра, опущенного из точки на прямую.

Проведем перпендикуляр из точки A на ребро двугранного угла и отметим точку их пересечения т.B.  ΔABO прямоугольный.

AB = 9.

Отрезок A₁B также перпендикулярен ребру двугранного угла (по теореме о трех перпендикулярах),

и A₁B = 9, (так как BO является медианой и высотой ΔABA₁, то ΔABA₁ равнобедренный).

• Градусной мерой двугранного угла называется градусная мера его линейного угла.

• Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях (линейный угол двугранного угла).

∠ABA₁ = φ, это линейный угол двугранного угла.

Для нахождения Cos ∠φ воспользуемся теоремой косинусов для равнобедренного треугольника ABA₁.

Значение косинуса угла φ положительно, значит двугранный ∠φ острый.