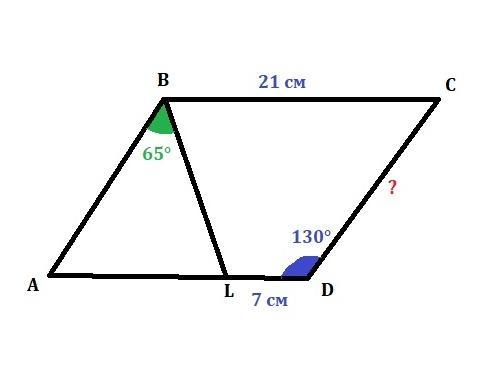
Дан параллелограмм ABCD, ∠D=130∘, BC=21 . На стороне AD есть такая точка L, что ∠ABL=65∘, LD=7. Найдите длину CD.

Ответ:

14 см

Объяснение:

ABCD - параллелограмм

Свойства параллелограмма:

• Противоположные стороны параллелограмма равны: АВ=CD, BC=AD
• Противоположные углы параллелограмма равны: ∠АВС = ∠ADС
• Сумма соседних равна 180°.

∠АВС = ∠ADС = 130°

∠LBC = 130°-∠АВL = 130-65=65°

∠ALB=∠LBC = 65° - как внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущей BL.

Так как ∠ALB = ∠АВL, то треугольник АВL - равнобедренный.

По свойству равнобедренного треугольника: АВ=АL

АВ=АL =AD - LD = ВС - LD = 21-7 = 14 см

Следовательно CD = АВ = 14 см - как стороны параллелограмма