Предмет: Математика, автор: sp09092005

решите неравенство 11х+7<=6(х+2) с решением

Ответы

Автор ответа: Alyssa08

Ответ:

$x \in (- \infty; 1]$ или $x \leq 1$

Пошаговое объяснение:

Рассмотрим правила решения неравенств на данном примере:

Любой член неравенства можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

Раскроем скобки в правой части неравенства и применим выше представленное правило неравенства:

$11x + 7 \leq 6 \cdot x + 6 \cdot 2$

$11x + 7 \leq 6x + 12$

$11x - 6x \leq 12-7$

$5x \leq 5$

Обе части неравенства можно умножать или делить на одно положительное число. Знак неравенства при этом не меняется:

$5x : 5 \leq 5 : 5$

$x \leq 1$

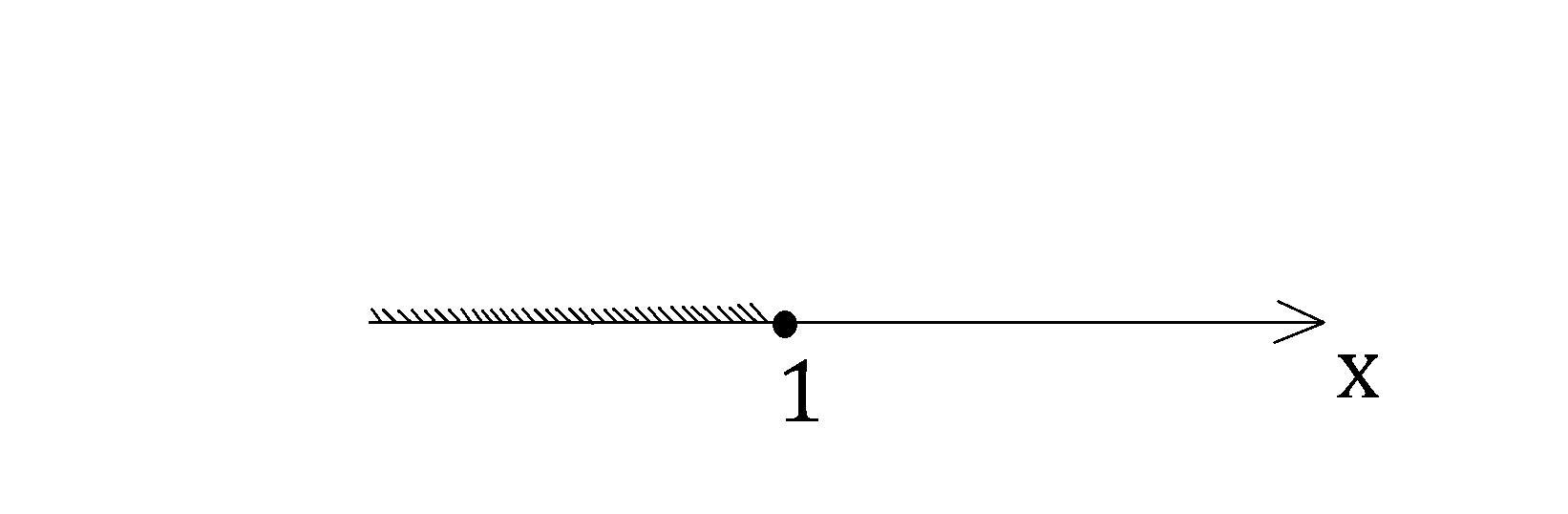
Начертим картинку данного неравенства.

Точка закрашенная, так как $\leq$ - знак нестрогий.

Штриховка пошла в левую часть, так как x МЕНЬШЕ или равно 1, а меньше - это то, что левее.

Запишем ответ в виде числового промежутка:

$x \in (- \infty; 1]$

В начале перед $- \infty$ круглая скобка, так как бесконечность всегда в круглых скобках. Это связано с тем, что неизвестно, какой аргумент мы возьмём.