Предмет: Математика,
автор: Аноним
Мат анализ 2 срочно!
100 баллов
Приложения:
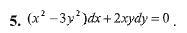
Ответы
Автор ответа:
2
Ответ:
разделим на х^2
Это однородное ДУ.
Замена:
общее решение
Автор ответа:
2
Интересные вопросы
Предмет: Математика,
автор: zlataleon
Предмет: Алгебра,
автор: GIRL99love
Предмет: Русский язык,
автор: zhibenya
Предмет: Химия,
автор: Sunlight11
Предмет: Математика,
автор: Аноним