Высота конуса равна 24,а радиус основания равен 10.Найдите площадь полной поверхности конуса​

Ответ:

S =  360·π ед².

Объяснение:

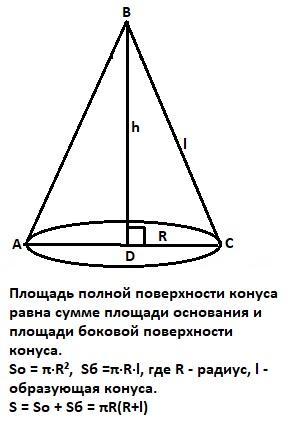
Площадь полной поверхности конуса равна сумме площади основания и площади боковой поверхности конуса.

So = π·R²,  Sб =π·R·l, где R - радиус, l - образующая конуса.

S = So + Sб = πR(R+l)

Образующую конуса найдем из прямоугольного треугольника с катетами: радиус и высота конуса.

l = √(R²+ h²) = √(100 + 576) = √676 = 26 ед.

Тогда S = πR(R+l) = π·10(10+26) = 360·π ед².