Предмет: Математика, автор: tor532751

Вычислите определенные интегралы, используя замену переменной.

Приложения:

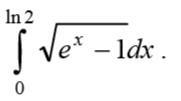
Ответы

Автор ответа: Miroslava227

1

Ответ:

замена:

${e}^{x} - 1 = t \\ {e}^{x} = t + 1 \\ {e}^{x} dx =dt \\dx = \frac{dt}{ {e}^{x} } = \frac{dt}{t + 1} \\ t1 = {e}^{ ln(2) } - 1 =2 - 1 = 1 \\ t2 = {e}^{0} - 1 = - 1$

$\int\limits \frac{ \sqrt{t} dt}{t + 1} \\$

делаем еще одну замену:

$\sqrt{t} = u \\ t = {u}^{2} \\ dt = 2udu$

Замену переменных делать не будем, так как один из пределов равен корню из (-1). В Полученный интеграл подставим все замены и тогда найдем численное решение.

$\int\limits \frac{u \times 2udu}{ {u}^{2} + 1 } = 2\int\limits \frac{ {u}^{2} }{ {u}^{2} + 1} du = \\ = 2\int\limits \frac{ {u}^{2} + 1 - 1 }{ {u}^{2} + 1} du = \\ = 2\int\limits \: du - 2\int\limits \frac{du}{ {u}^{2} +1 } = \\ = 2u - 2arctg(u) + C= \\ = 2(u - arctg(u)) + c=2(\sqrt{{e}^{x}-1}-arctg(\sqrt{{e}^{x}})+C$

подставляем пределы:

$2(1-arctg(\sqrt{1})-(0-arctg({\sqrt{-1}}))=\\=2(1-\frac{\pi}{4})=2-\frac{\pi}{2}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Геометрия, автор: diankagorkova

Основания трапеции относятся как 4:5. Средняя линия равна 54. Найти меньшее основание трапеции.

2 года назад

Предмет: Математика, автор: katrinakukina2004

Из города А в город В выехала машина. Если она будет ехать со скоростью 70 км/ч, то опозданием 2 часа, если будет ехать со скоростью 80 км/ч, то приедет на 1 час раньше срока. Определи расстояние между городами А и В

2 года назад

Предмет: Русский язык, автор: 6000ЛАРАПОЛИНА

корень -БАГР- красный цвет обазначающий

2 года назад

Предмет: Математика, автор: bodnarhuk83

Допоможіть скласти короткий запис задачі. У шести однакових банках вміщується 18 л соку. Місткість сулії на 5 літрів більша від місткості банки. Скільки літрів соку вміститься у вісьми таких суліях?

8 лет назад

Предмет: Химия, автор: kkurlyukova2003

Срочно очень это химия 8 класс

8 лет назад