Предмет: Математика, автор: mrsignalka

найти производные Х y(штрих) , пользуясь правилами и формулами дифференцирования.

Приложения:

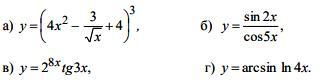
Ответы

Автор ответа: Miroslava227

1

Ответ:

а)

$y' = 3 {(4 {x}^{2} - \frac{3}{ \sqrt{x} } + 4)}^{2} \times (8x - 3 \times ( - \frac{1}{2} ) {x}^{ - \frac{3}{2} } ) = \\ = 3(8x + \frac{3}{2x \sqrt{x} } ) {(4 {x}^{2} - \frac{3}{ \sqrt{x} } + 4)}^{2}$

б)

$y' = \frac{2 \cos(2x) \times \cos(5x) - ( - 5 \sin(5x)) \times \sin(2x) }{ { \cos }^{2} (5x)} = \\ = \frac{2 \cos(2x) }{ \cos(5x) } + \frac{5 \sin(5x) \sin(2x) }{ { \cos}^{2}(5x) } = \\ = \frac{2 \cos(2x) }{ \cos(5x) } + \frac{5tg(5x) \sin(2x) }{ { \cos}(5x)} = \\ = \frac{ \cos(2x) + 5 \sin(2x) tg(5x)}{ \cos(5x) }$

в)

$y' = ln(2) \times {2}^{8x} \times 8tg(3x) + \frac{1}{ { \cos }^{2} (3x)} \times 3 \times {2}^{8x} = \\ = {2}^{8x} (8 ln(2) \times tg(3x) + \frac{3}{ { \cos }^{2} (3x)} )$

г)

$y' = \frac{1}{ \sqrt{1 - {ln}^{2} (4x)} } \times \frac{1}{4x} \times 4 = \\ = \frac{1}{ \sqrt{1 - {ln}^{2} (4x)} }$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Геометрия, автор: elviraganieva

Что такое накрест лежащие соответственный и внутренние однотонные углы? ПОМОГИТЕ ПОЖАЛУЙСТА

2 года назад

Предмет: Математика, автор: Катя20042004

На открытку папе к 23 февраля Лена решила наклеить красную ленточку в форме пятиконечной звезды.Сколько дециметров ленты потребуется Лене,ЕСЛИ ДЛИНА
ОДНОГО ЗВЕНА ЛОМАНОЙ 3 См?

2 года назад

Предмет: Геометрия, автор: kapchunova2011

Величины двух углов параллелограмма относятся как 4:5.Чему равны все углы параллелограмма?

2 года назад

Предмет: Математика, автор: kirillru2

Помогите решить уравнение (х-506)+215=429

8 лет назад

Предмет: История, автор: SoapyLemmons

50 баллов. Кому не лень.
Напишите маленький конспект по человеку Данте Алигьери. Отчасти и инета и отчасти перефразируйте своими словами. Кто он такой и чем занимался. Только на 8-10 предложений. Заранее спасибки.

8 лет назад