![\sqrt[? \\3 \\ \\ \frac{ {?}^{?} \times \frac{?}{?} \times \frac{?}{?} \times \frac{?}{?} \times \frac{?}{?} }{?} ]{?} \sqrt[? \\3 \\ \\ \frac{ {?}^{?} \times \frac{?}{?} \times \frac{?}{?} \times \frac{?}{?} \times \frac{?}{?} }{?} ]{?}](https://tex.z-dn.net/?f=+%5Csqrt%5B%3F+%5C%5C3+%5C%5C++%5C%5C++%5Cfrac%7B+%7B%3F%7D%5E%7B%3F%7D++%5Ctimes+%5Cfrac%7B%3F%7D%7B%3F%7D++%5Ctimes+%5Cfrac%7B%3F%7D%7B%3F%7D++%5Ctimes+%5Cfrac%7B%3F%7D%7B%3F%7D++%5Ctimes+%5Cfrac%7B%3F%7D%7B%3F%7D+%7D%7B%3F%7D+%5D%7B%3F%7D+)
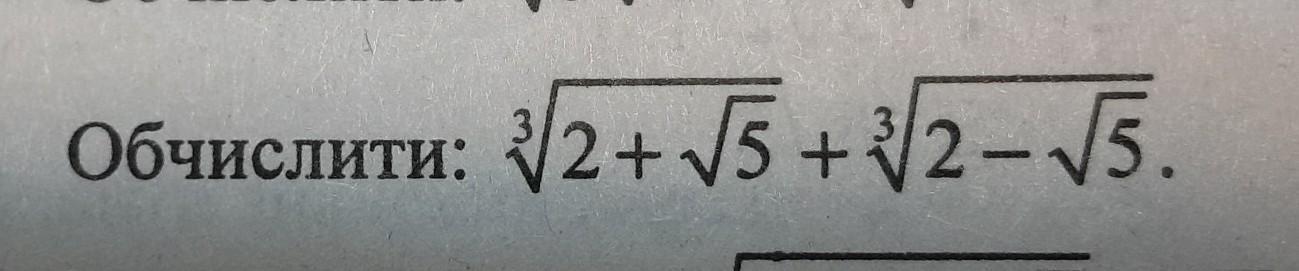
Ответы
Ответ:
Пошаговое объяснение:
всё будет очень долго. если не зависнет программа запишу
поехали
1) приравняем выражение к Х и возведем всё в 3 степень
(когда найдем Х - получим решение для нашего примера)
теперь по обычной формуле (а+b)³ = a³ +b³ +2a²b +2ab² возводим в куб левую часть
первые два члена возводим в куб, а из второго и третьего выносим за скобки общий множитель
теперь самое аккуратное
1. +√5 и -√5 сокращаются
2. +2 и +2 дадут 4
3. там, где выносили общий множитель все внесем под знак корня
под корнем получили разность квадратов
4. теперь вспоминаем что
и вот проведя все эти преобразования мы получим вот что
это будет простое кубическое уравнение
Х³ +3Х -4 = 0; заменим 3Х на 4Х -Х
Х³ -Х +4Х-4 = Х³ -Х +4Х -4 = Х(Х² -1) + 4(Х -1)= (Х-1)(Х² +Х +4)
нам надо найти Х, значит приравняем вырахение к 0
(Х-1)(Х² +Х +4)=0
первый корень из (Х-1) будет Х = 1
(Х² +Х +4) - это квадратное уравнение корней не имеет.
вот и всё. мы нашли, чему равно наше исходное выражение