Предмет: Математика, автор: Аноним

Задание 2. Решите простейшие тригонометрические уравнения

Приложения:

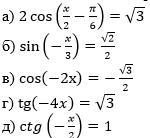
Ответы

Автор ответа: Miroslava227
0

Ответ:

а)

2 \cos( \frac{x}{2} - \frac{\pi}{6} ) = \sqrt{3} \\ \cos( \frac{x}{2} - \frac{\pi}{6} ) = \frac{ \sqrt{3} }{2} \\ \\ \frac{x1}{2} - \frac{\pi}{6} = \frac{\pi}{6} + 2\pi \: n \\ \frac{x1}{2} = \frac{\pi}{3} + 2\pi \: n \\ x1 = \frac{2\pi}{3} + 4 \pi \: n \\ \\ \frac{x2}{2} - \frac{\pi}{6} = - \frac{\pi}{6} + 2\pi \: n \\ \frac{x2}{2} = 2\pi \: n \\ x2 = 4\pi \: n

n принадлежит Z.

б)

\sin( - \frac{x}{3} ) = \frac{ \sqrt{2} }{2} \\ \\ - \frac{x1}{3} = \frac{\pi}{4} + 2\pi \: n \\ x1 = - \frac{3\pi}{4} + 6\pi \: n \\ \\ - \frac{x2}{3} = \frac{3\pi }{4} + 2\pi \: n \\ x2 = - \frac{9\pi}{4} + 6\pi \: n

n принадлежит Z.

в)

\cos( - 2x) = - \frac{ \sqrt{3} }{2} \\ \\ 2x1 = \frac{5 \pi}{6} + 2\pi \: n \\ x1 = - \frac{5\pi}{12} + \pi \: n \\ \\ - 2x2 = - \frac{5\pi}{6} + 2\pi \: n \\ x2 = \frac{5\pi}{12} + \pi \: n

n принадлежит Z.

г)

tg( - 4x) = \sqrt{3} \\ - 4x = \frac{\pi}{3} + \pi \: n \\ x = - \frac{\pi}{12} + \frac{\pi \: n}{4}

n принадлежит Z.

д)

ctg( - \frac{x}{2} ) = 1 \\ \cos( - \frac{x}{2} ) = 1 \\ - \frac{x}{2} = 2\pi \: n \\ x = - 4\pi \: n

n принадлежит Z.

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Английский язык, автор: anna1605m
нужна отгадка к загадке.I am nice,but i am not big.I can fly and sing.I am red and black,i can ride a cat.
2 года назад
Предмет: Химия, автор: anacondaVIP
помогите пожалуйста с химией.Хотя бы одну задачу!Срочно!
2 года назад
Предмет: Другие предметы, автор: Мария0086
ИМЯ УЧЁНОГО КОТОРЫЙ ИССЛЕДОВАЛ НЕФТЯНЫЕ МЕСТОРОЖДЕНИЯ РОССИИ 6 БУКВ НАЧИНАЕТСЯ НА Г
2 года назад
Предмет: Математика, автор: Аноним
Какое из чисел является решением (корнем) уравнения? 512:х-100=28
8 лет назад
Предмет: Математика, автор: Iren222
При декурсивном способе расчета сложных процентов по годовой процентной ставке наращивания (р) с увеличением числа (m) периодов начисления в году через (n) лет общая сумма процентного дохода:
а) Увеличивается;
б) Уменьшается;
в) остается постоянной
8 лет назад