Предмет: Математика, автор: orcahaken0232

Найдите производные функции

Приложения:

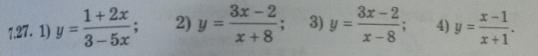
Ответы

Автор ответа: Miroslava227

Ответ:

по формуле:

$( \frac{u}{v} )' = \frac{u'v - v'u}{ {v}^{2} } \\$

$1)y '= \frac{2(3 - 5x) - ( - 5)(1 + 2x)}{ {(3 - 5x)}^{2} } = \\ = \frac{6 - 10x + 5 + 10x}{ {(3 - 5x)}^{2} } = \frac{11}{ {(3 - 5x)}^{2} }$

$2)y' = \frac{3(x + 8) - (3x - 2)}{ {(x + 8)}^{2} } = \\ = \frac{3x + 24 - 3x + 2}{ {(x + 8)}^{2} } = \frac{26}{ {(x + 8)}^{2} }$

$3)y '= \frac{3(x - 8) - (3x - 2)}{ {(x - 8)}^{2} } = \\ = \frac{3x - 24 - 3x + 2}{ {(x - 8)}^{2} } = - \frac{22}{ {(x - 8)}^{2} }$

$4)y' = \frac{x + 1 - (x - 1)}{ {(x + 1)}^{2} } = \\ = \frac{x + 1 - x + 1}{ {(x + 1)}^{2} } = \frac{2}{ {(x + 1)}^{2} }$

Интересные вопросы

Предмет: История, автор: Mari12161

2 года назад

Предмет: Русский язык, автор: tractorist04048

2 года назад

Предмет: Українська література, автор: No1zyBoy

2 года назад

Предмет: Физика, автор: mashasam2000

8 лет назад

Предмет: Математика, автор: светсаня1375

8 лет назад