Предмет: Алгебра, автор: Аноним

РЕШИТЕ должно рациональное уравнение умаляю

Приложения:

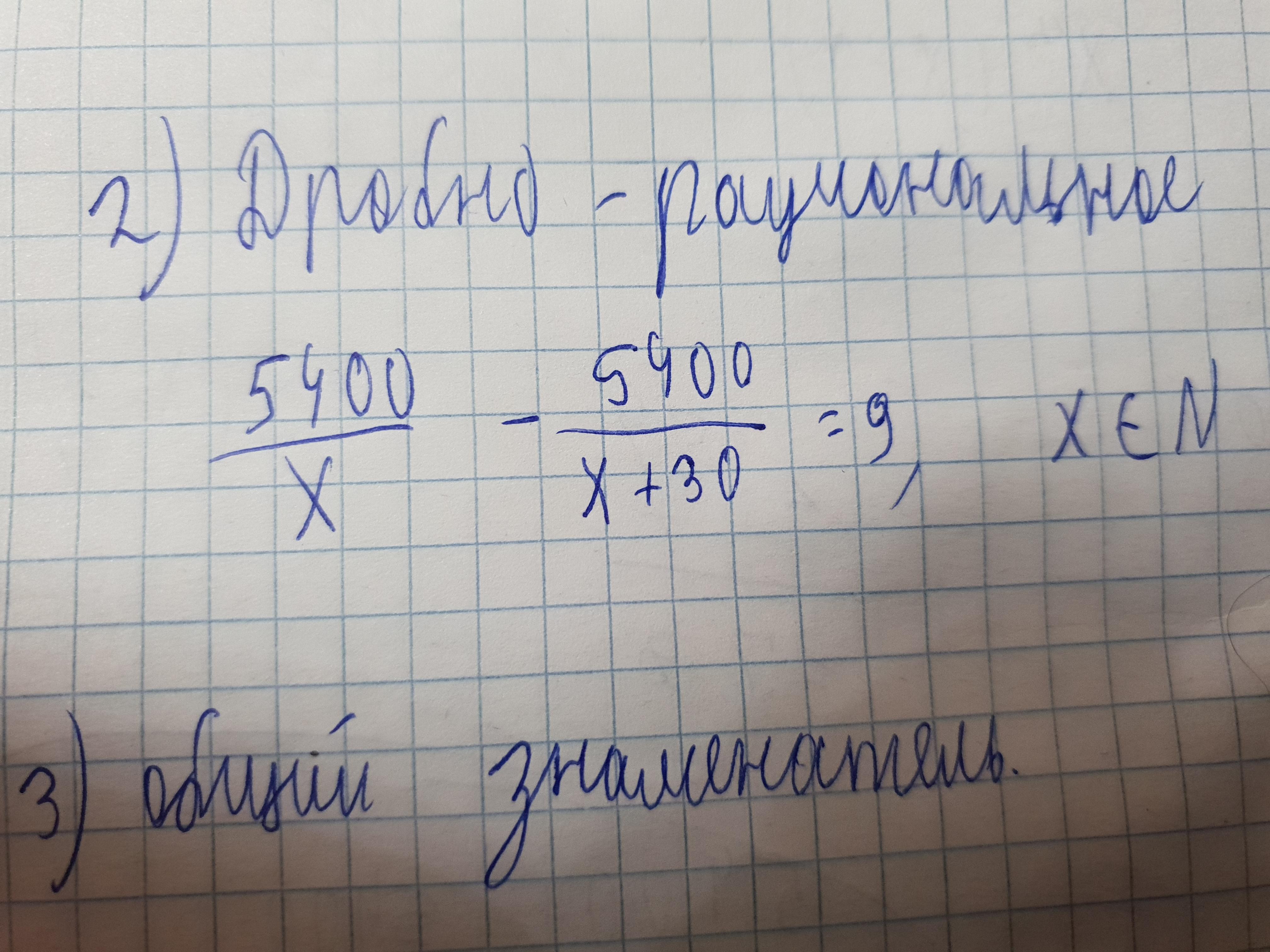
Ответы

Автор ответа: Аноним

1

$\frac{5400}{x} - \frac{5400}{x + 30} - 9 = 0 \\ \frac{5400(x + 30) - 5400x - 9x \times (x + 30)}{x(x + 30)}$

$\frac{5400x + 162000 - 5400x - 9x {}^{2} - 270x }{x(x + 30)} \\ \frac{162000 - 9x {}^{2} - 270x}{x(x + 30)} = 0 \\ 162000 - 9x {}^{2} - 270x = 0 \\ - 9x {}^{2} - 270x + 162000 = 0 \\ x {}^{2} + 30x - 18000 = 0$

$x {}^{2} + 150x - 120x - 18000 = 0 \\ x(x + 150) - 120(x + 150) = 0 \\ (x + 150)(x - 120) = 0 \\$

$x + 150 = 0 \\ x - 120 = 0 \\$

$x = - 150 \\ x = 120$

$x1 = - 150 \\ x2 = 120$

Общий знаменатель:

$x(x + 30)$

Автор ответа: MatemaT123

0

Ответ:

$120;$

$x(x+30);$

Объяснение:

ОДЗ:

$x \neq 0, \quad x \neq -30, \quad x \in \mathbb {N};$

Решение:

$\frac{5400}{x}-\frac{5400}{x+30}=9 \quad | \quad \cdot x(x+30) \neq 0$

$5400(x+30)-5400x=9x(x+30);$

$5400x+162000-5400x=9x^{2}+270x;$

$9x^{2}+270x-162000=0 \quad | \quad :9$

$x^{2}+30x-18000=0;$

$D=b^{2}-4ac;$

$D=30^{2}-4 \cdot 1 \cdot (-18000)=900+72000=72900=270^{2};$

$x_{1}=\frac{-b+\sqrt{D}}{2a} \Rightarrow x_{1}=\frac{-30+\sqrt{270^{2}}}{2 \cdot 1}=\frac{-30+270}{2}=\frac{240}{2}=120;$

$x_{2}=\frac{-b-\sqrt{D}}{2a} \Rightarrow x_{2}=\frac{-30-\sqrt{270^{2}}}{2 \cdot 1}=\frac{-30-270}{2}=\frac{-300}{2}=-150;$

Второй корень не удовлетворяет ОДЗ.

3) общий знаменатель:

$x(x+30).$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Математика, автор: Risk14

Вроде легкое задание, но не решить. Определение даже дам: Если множеством значений случайной величины является конечное (или
счетное) множество чисел, не имеющее предельной точки, то такие случайной величины называются дискретными.
Задание:
Какая из указанных ниже случайных величин является дискретной?
Выберите один ответ:
1. Количество выпавших очков при игре в рулетку
2. Координата пробоины в мишени
3. Угол, на который повернется стрелка рулетки
4. Масса наудачу взятой снежинки

2 года назад

Предмет: Математика, автор: Azamat200410

Найди значение выражение. a+4a+15a, при a = 202. 45x-23x-x,при x = 1234. 345y-234y+y = 23. 1000z-635z+z, при z = 12

2 года назад

Предмет: Математика, автор: megalaz

Половину пути велосипедист проехал за 2 часа со скоростью 15 км/ч,а остальной путь -со скоростью 10 км/ч.Сколько времени велосипедист был в пути?

2 года назад

Предмет: Биология, автор: kelizaveta859

Почему транспорт веществ-важнейший процесс жизнедеятельности организмов?

8 лет назад

Предмет: География, автор: jora2030

Помогите, пожалуйста!!! Период в истории до эпохи Великих географических открытий.

8 лет назад