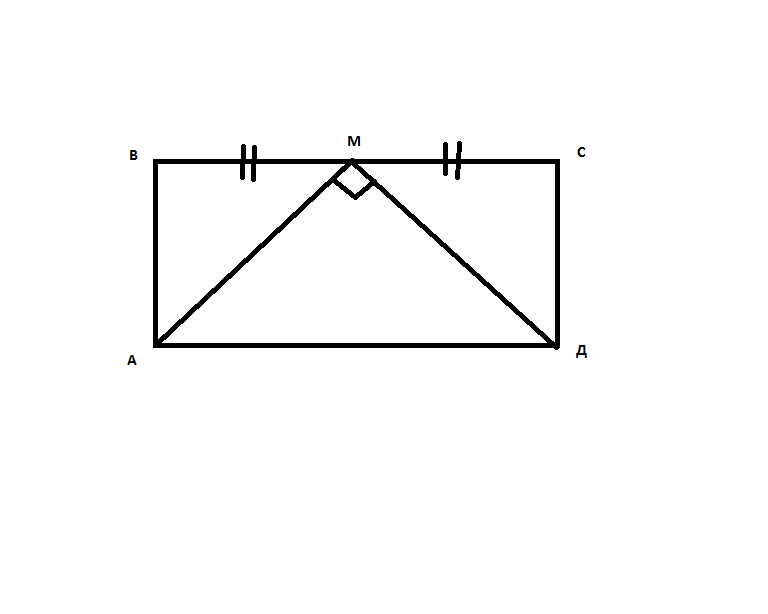
В прямоугольнике ABCD M-середина BC, прямые MA и MD взаимно перпендикулярны, периметр прямоугольника ABCD=24м.
Доказать, что треугольник AMD-равнобедренный))))
И рисунок и кзадаче пожалуйста..) Спасибо ипобыстрее

треугольник АВМ = треугольнику МСД по 1 признаку (уголВ=углуС=90градусов, т.к. углы прямоугольника, ВМ=МС по условию, АВ=СД т.к. противоположные стороны прямоугольника равны). Следовательно, АМ=МД, следовательно, треугольник АМД равнобедренный.

АВ=СД- ширина прямоуг АВСД
Вм=МС  ( М -середина ВС)
Рассм АВМ и МСД- прямоугольные треуг-ки,
угол С=Углу В=90гр
По двум сторонам и углу между ними, треугольники равны, след-но и АМ и МД тоже равны. Значит тр-к АМД равноб.

только непонятно для чего дан периметр