Помогите пожалуйста ОЧЕНЬ СРОЧНО!!! Точка D рівновіддалена від вершин рівностороннього трикутника ABC. Знайдіть кут між площинами ABC i ABD, якщо АВ=12 см, а точка D віддалена від площини АВС на 2 см.

Точка D равноудалена от вершин равностороннего треугольника АВС. Найти угол между плоскостями АВС и ABD, если АВ = 12 см, а точка D удалена от плоскости АВС на 2 см.

Ответ:

30°

Объяснение:

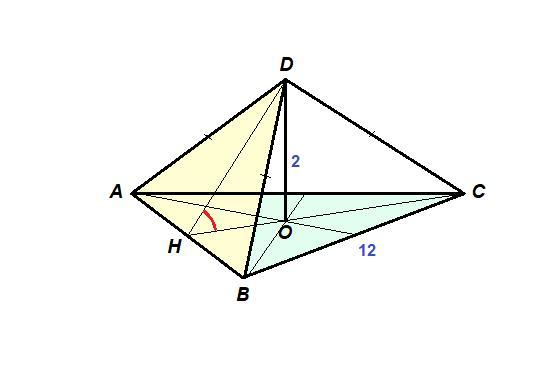
Проведем DO⊥(ABC). DO = 2 см - расстояние от точки D до плоскости (АВС).

ΔADO = ΔBDO = ΔCDO по гипотенузе и катету, так как

• ∠AOD = ∠BOD = ∠COD = 90° (отрезок DO перпендикулярен любой прямой плоскости (АВС));
• DA = DB = DC по условию (точка D равноудалена от вершин ΔАВС);
• DO - общий катет.

Значит, АО = ВО = СО и О - центр правильного треугольника.

Пусть Н - середина АВ.

СН⊥АВ как медиана и высота равностороннего треугольника АВС,

DH⊥АВ как медиана и высота равнобедренного треугольника DАВ,

значит ∠DHO - линейный угол двугранного угла между плоскостями (АВС) и (ABD).

как радиус окружности, вписанной в равносторонний треугольник.

см

ΔDHO:  ∠DOH = 90°,

∠DHO = 30°