1) Сторона ромба равна 20 см, а одна из его диагонали равна 32 см. Найдите длину второй диагонали.
2) В окружности с радиусом 5 см проведена хорда, равна 8 см. Найдите длину отрезка, соединяющего центр окружности с середины хорды.
(С рисунками пожалуйста)

Ответ:

Объяснение:

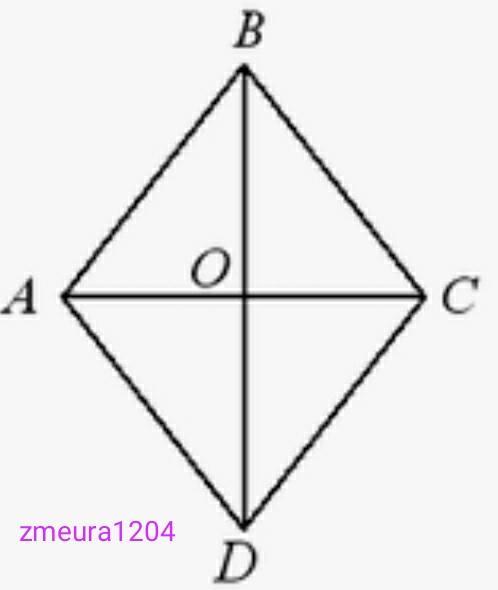
Дано:

ABCD- ромб

АВ=20см

ВD=32см

АС=?

Решение

Диагонали ромба пересекаются перпендикулярно и точкой пересечения делятся пополам.

ВО=ВD:2=32:2=16см.

∆АОВ- прямоугольный треугольник.

По теореме Пифагора

АО=√(АВ²-ВО²)=√(20²-16²)=√(400-256)=

=√144=12см.

АС=2*АО=2*12=24см.

Ответ: АС=24см.

2)

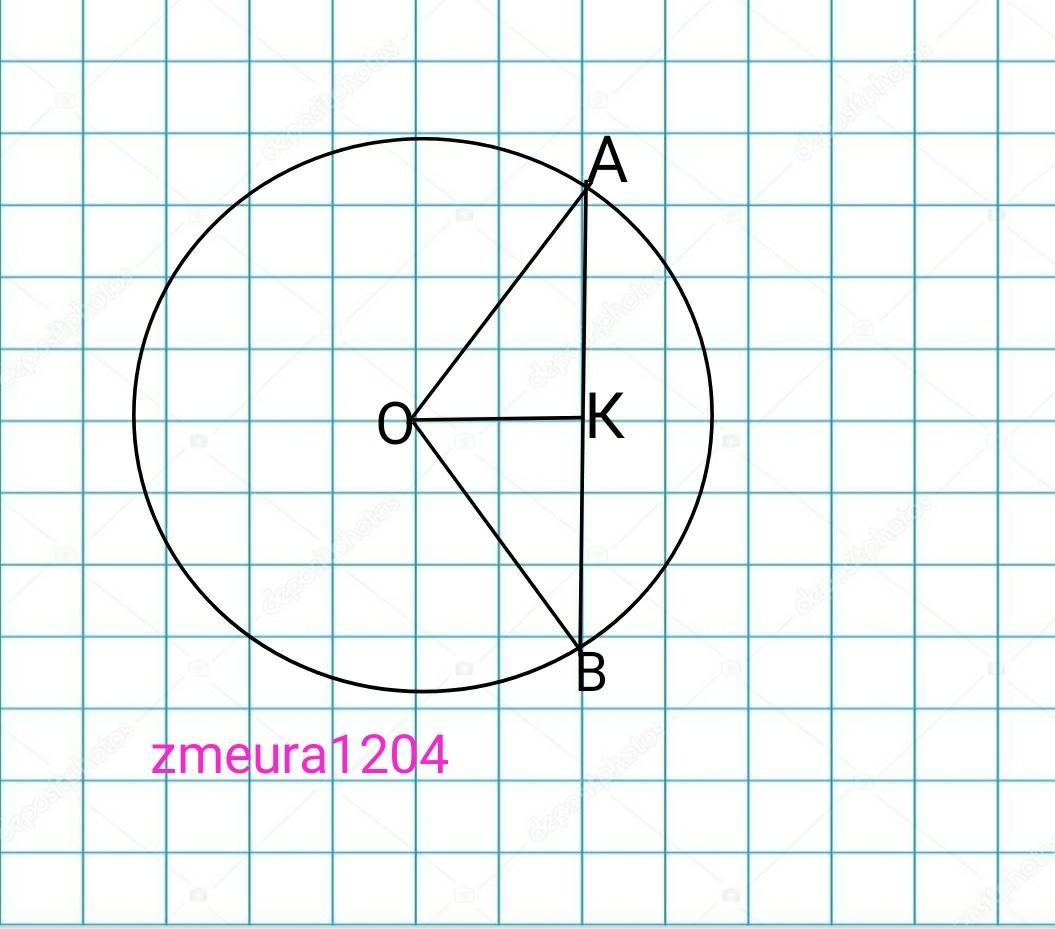
Дано:

Окружность

О-центр окружности

АВ=8см хорда

ОА=ОВ=R=5см

ОК=?

Решение

ОК- высота, медиана и биссектрисса равнобедренного треугольника ∆АОВ.

ВК=КА

ВК=АВ:2=8:2=4см.

Теорема Пифагора

ОК=√(ОВ²-КВ²)=√(5²-4²)=√(25-16)=3см

Ответ: 3см