Предмет: Геометрия,
автор: olgadyra12
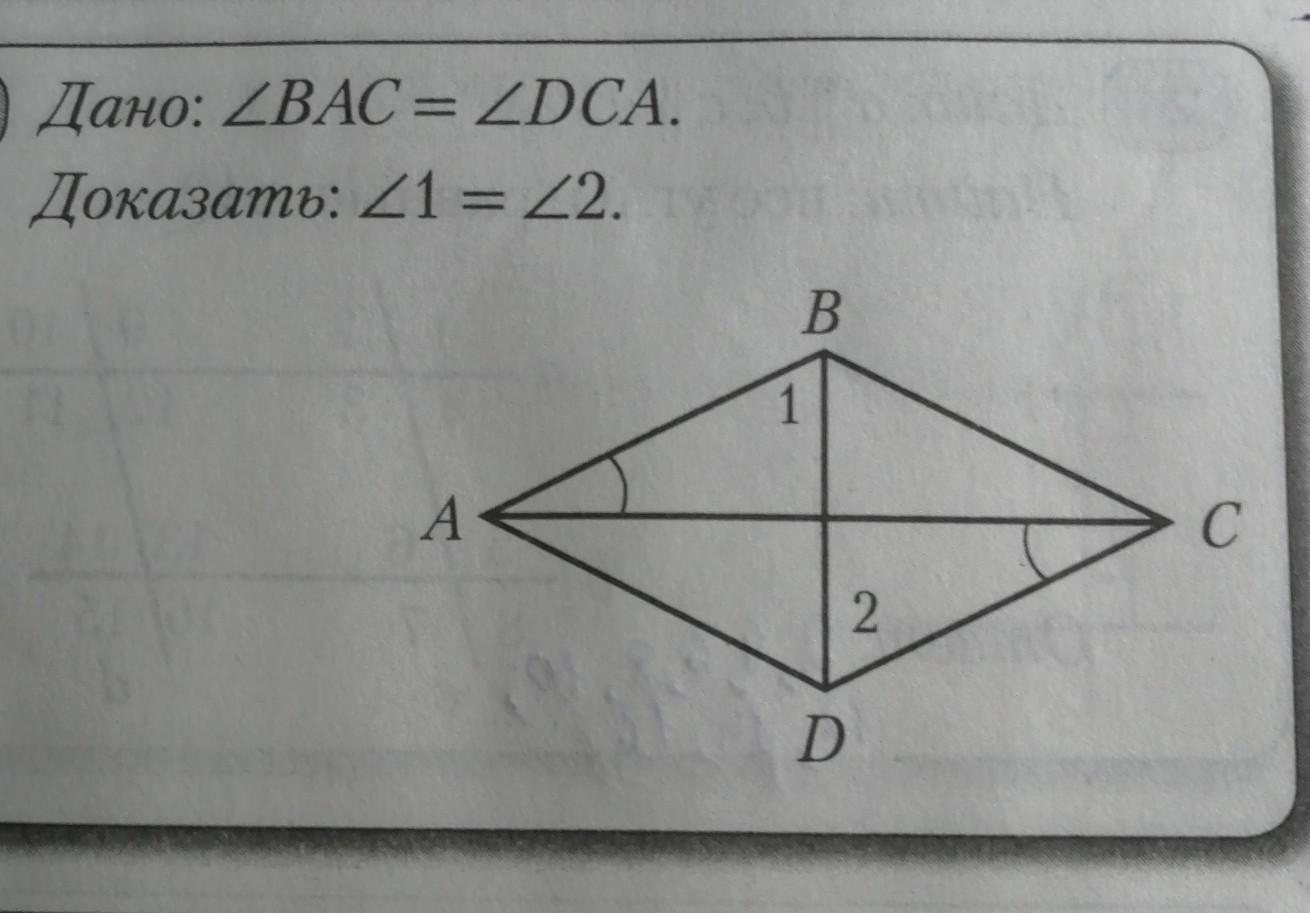
Дано: <BAC = <DCA.
Доказать: <1 = <2
Приложения:
Ответы
Автор ответа:
0
Ответ:
∠ 1 = ∠ 2 как накрест лежащие углы
Объяснение:
∠ BAC и ∠ DCA образованы при пересечении прямых AB и DC секущей AC. Поэтому ∠ BAC и ∠ DCA - это внутренние накрест лежащие углы.
Если накрест лежащие углы, образующиеся при пересечении двух
прямых секущей, равны, то прямые параллельны.
∠ BAC = ∠ DCA ⇒ AB || DC
∠ 1 и ∠ 2 образованы при пересечении прямых AB и DC секущей BD.
Поэтому ∠ 1 и ∠ 2 - это внутренние накрест лежащие углы.
Так как мы установили, что AB || DC, то ∠ 1 = ∠ 2 (Если две параллельные прямые пересечены секущей, то углы, образующие пару накрест лежащих углов, равны), что и требовалось доказать.
Интересные вопросы
Предмет: Химия,
автор: Ruslan252162
Предмет: Информатика,
автор: tujhgbljh
Предмет: Алгебра,
автор: cthmuf
Предмет: Русский язык,
автор: zhawe