Предмет: Алгебра, автор: zhannazr

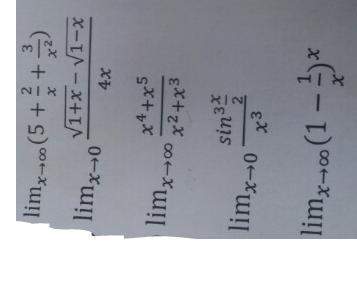
Помогите решить пределы пожалуйста!

Приложения:

Ответы

Автор ответа: pushpull

1

Ответ:

Объяснение:

1. $\displaystyle \lim_{x \to \infty} (5+\frac{2}{x} +\frac{3}{x^2} ) = 5+0+0=5$

2. умножаем числитель и знаменатель на сопряденное для числителя выражение

$\displaystyle \lim_{x \to 0} \frac{(\sqrt{1+x}-\sqrt{1-x})(\sqrt{1+x}+\sqrt{1-x} ) }{4x( \sqrt{1+x}+\sqrt{1-x} )} = \lim_{x \to 0} \frac{2x}{4x(\sqrt{1+x}+\sqrt{1-x} ) } =$

$\displaystyle = \lim_{x \to 0} \frac{1}{2(\sqrt{1+x}+\sqrt{1-x}) } = \frac{1}{4}$

3. в числителе выносим за скобки х⁵ в знаменателе х³

$\displaystyle \lim_{x \to \infty} \frac{x^4+x^5}{x^2+x^3} = \lim_{x \to \infty} \frac{x^5}{x^3} *\frac{1+\frac{1}{x^2} }{1+\frac{1}{x} } = \lim_{x \to \infty} x^2=\infty$

4. употребим следствие свойств первого замечательного предела

$\displaystyle sin \bigg (\frac{x}{2} \bigg ) \approx \frac{x}{2}$

тогда предел примет вид

$\displaystyle \lim_{x \to 0} \bigg (\frac{x^3}{8x^3} \bigg )= \frac{1}{8}$

5. здесь используем второй замечательный предел

$\displaystyle \lim_{x \to \infty} \bigg (1+\frac{a}{x} \bigg )^{bx}=e^{bx}$

у нас тут а = -1; b = 1

$\displaystyle \lim_{x \to \infty} \bigg (1+\frac{-1}{x} \bigg )^{x}=e^{-1}$

zhannazr: все написала в коментарии к вопросу

zhannazr: помги пожалуйста(((

zhannazr: пожалуйста помоги ,хочется жить(((

zhannazr: я все уточнила , помоги пожалуйста(

zhannazr: помоги пожалуйста

pushpull: ну и фигнень.... до сих пор считала... но, слава Богу, сделала....

pushpull: тьфу на этих преподов, которые такое задают.... (((((

pushpull: забирайте эту хренотень.....

zhannazr: Спасибо , тебе огромное!!! очень помогла!!!

pushpull: пожалуйста -))

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: География, автор: Аноним

Градусная сеть на глобусе и карте

2 года назад

Предмет: Математика, автор: lIZgunariys

Площадь территории Италии составляет 301 тыс. км в квадрате, как эта величина записывается в стандартном виде?(Ребята мне срочно нужно может кто знает?)
1.3,01*10^6
2.3,01*10^7
3.3,01*10^5
4.3,01*10^4

2 года назад

Предмет: Информатика, автор: Аноним

если положительный ответ на какой-то вопрос можно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно быстро найти (за полиномиальное время и используя полиномиальную память)? Другими словами, действительно ли решение задачи проверить не легче, чем его отыскать?
Например, верно ли, что среди чисел {−2, −3, 15, 14, 7, −10, …} есть такие, что их сумма равна 0 (задача о суммах подмножеств)? Ответ да, потому что −2 −3 + 15 −10 = 0 легко проверяется несколькими сложениями (информация, необходимая для проверки положительного ответа, называется сертификатом). Следует ли отсюда, что так же легко подобрать эти числа?

2 года назад

Предмет: Математика, автор: kxkxkks

1. Округлите до единиц:
А)34,35
Б)203,45
В)3,801
Г) 2005,8

2. Округлите до десятых.
А)0,84
Б) 234,182
В)23,673
Г)0,77

8 лет назад

Предмет: Математика, автор: konovalovdana22ь

помогите с задачими В театральной кассе 1300 билетов.В первый день продали 270 билетов,а во второй - на 150 билетов больше.Сколько билетов осталось в кассе.

На телеграфе отправили 910 срочных телеграмм.Это в 7 раз больше,чем поздравительных телеграмм.Сколько всего телеграмм отправили на почте?

Детская площадка имеет длину 60м,а ширину 40м.При этом 2\8 площади занято горками,а остальная площадь различными качелями.Какая площадь занята качелями?

8 лет назад