Предмет: Алгебра, автор: 11Vbif

Система, состоящая из квадратного и рационального уравнений, метод умножения.

Приложения:

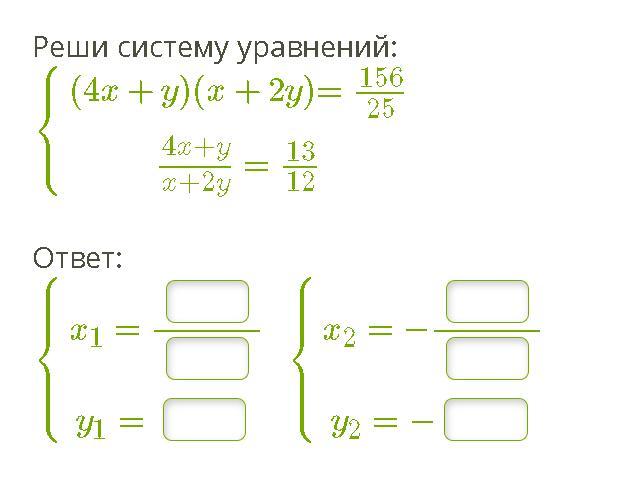
Ответы

Автор ответа: sangers1959

1

Объяснение:

$\left \{ {{(4x+y)*(x+2y)=\frac{156}{25} } \atop {\frac{4x+y}{x+2y}=\frac{13}{12} }} \right. .$

Пусть 4х+у=t, x+2y=v. ⇒

$\left \{ {{t*v=\frac{156}{25} } \atop {\frac{t}{v}=\frac{13}{12} }} \right. .$

Умножаем первое уравнение на второе:

$t^2=\frac{156*13}{25*12}=\frac{13*13}{25}=\frac{13^2}{5^2}=(\frac{13}{5})^2\\t_1=\frac{13}{5}\ \ \ \ \Rightarrow\\\frac{13}{5}*v =\frac{156}{25} \ |*\frac{5}{13}\\v=\frac{156*5}{25*13} =\frac{12}{5}.\\\left \{ {{4x+y=\frac{13}{5}\ |*10 } \atop {x+2y=\frac{12}{5}\ |*5 }} \right.\ \ \ \ \left \{ {{40x+10y=26} \atop {5x+10y=12}} \right..$

Вычитаем из первого уравнения второе:

$35x=14\ |:35\\x_1=\frac{2}{5}.\ \ \ \ \Rightarrow\\5*\frac{2}{5} +10y=12\\2+10y=12\\10y=10\ |:10\\y_1=1.$

$\\t_2=-\frac{13}{5}\ \ \ \ \Rightarrow\\-\frac{13}{5}*v =\frac{156}{25} \ |*\frac{5}{13}\\v=-\frac{156*5}{25*13} =-\frac{12}{5}.\\\left \{ {{4x+y=-\frac{13}{5}\ |*10 } \atop {x+2y=-\frac{12}{5}\ |*5 }} \right.\ \ \ \ \left \{ {{40x+10y=-26} \atop {5x+10y=-12}} \right..$

Вычитаем из первого уравнения второе:

$35x=-14\ |:35\\x_2=-\frac{2}{5}.\ \ \ \ \Rightarrow\\5*(-\frac{2}{5} ) +10y=-12\\-2+10y=-12\\10y=-10\ |:10\\y_2=-1.$

Ответ:

$\left \{ {{x_1=\frac{2}{5} } \atop {y=1}} \right. \ \ \left \{ {{x_2=-\frac{2}{5} } \atop {y_2=-1}.} \right.$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Химия, автор: maag

вывести формулу газообразного соединения массовая доля фосфора 91,18%, а водорода 8,82%. Относительная плотность его по кислороду равна 1,0625

2 года назад

Предмет: Химия, автор: obinbobin

алкадиены состав и строение

2 года назад

Предмет: Математика, автор: настюша678

Девочки составляют 5/9 учащихся класса. В различных спортивных секциях занимаются 3/4 мальчиков и 3/5 девочек класса. Определить, какая часть учащихся класса посещает спортивные секции.

Решите задачу! Ответ в книге 2/3.

2 года назад

Предмет: Русский язык, автор: самурай14

Просклоняйте:
В форме Р.П и П.П следущиее числительные.(Числа написать словами)
1635-ый год и 2018-ый год

8 лет назад

Предмет: Математика, автор: levkim01

Вычислите более удобным способом

8 лет назад