Предмет: Геометрия,
автор: MercurialX
диагонали трапеции MNKL основанием ML пересекаются в точке О. Найдите площадь треугольника MOL, если площадь треугольника NOK равна 75 см2, ML=9 см, NK=15 см
Ответы
Автор ответа:
1
Ответ:
Решение:
S (NOK) = 1/2 × OP × NK
75 = 1/2 × 15 × OP
OP = 10
ΔNOK ~ Δ MOL (Подобен), так как ∠NKM = ∠KML, ∠KNL = ∠NLM, NFR RFR NK ║ ML, а диагонали в роли секущих
Коэффициент подобия
NK/ML=OP/OR
15/9 = 10/OR
OR = (9×10) ÷15 = 6
S (MOL) = 1/2 ×6 × 9 = 27
Ответ: 27
Приложения:
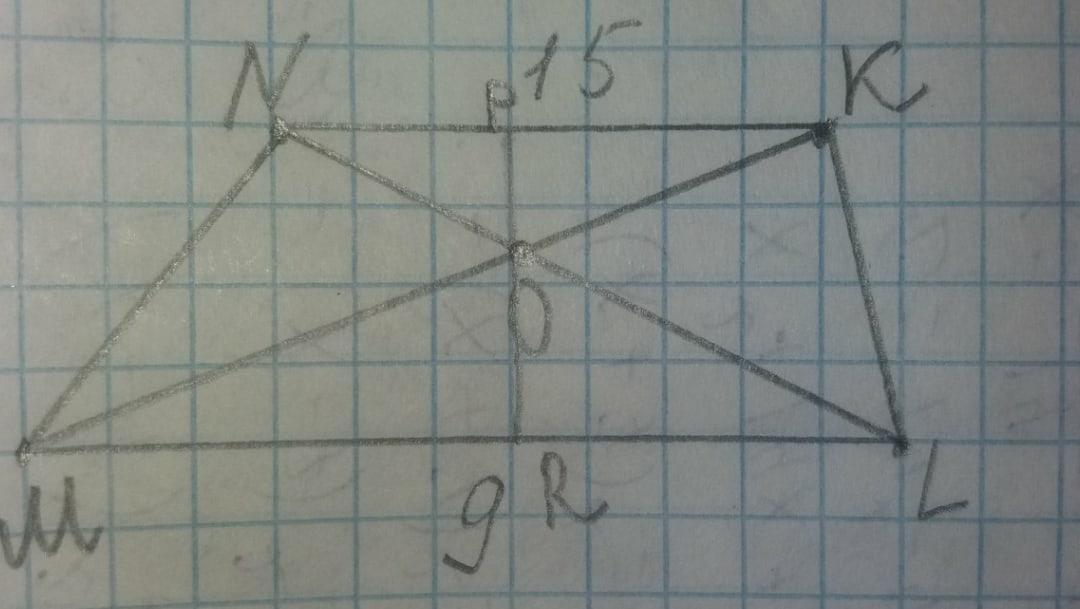
Интересные вопросы
Предмет: История,
автор: nika20907
Предмет: Русский язык,
автор: scleer
Предмет: Английский язык,
автор: Polinagodyna
Предмет: Математика,
автор: vavilova25101
Предмет: Русский язык,
автор: RabotniCHEK