Предмет: Геометрия, автор: 4585o7k5099

Задача на 60 баллов!
Дан остроугольный треугольник АВС. На нём отмечена точка Р так, что АР:РВ=2:3. АС=РС=1. Найти угол АСВ при котором площадь треугольника АВС максимальна.
Помогите

siestarjoki: Задача кажется очевидной, поэтому, возможно, в ней есть подвох, которого я не заметил.

4585o7k5099: Сможешь решить остальное на моей странице

Ответы

Автор ответа: siestarjoki

Треугольники ACP и ABC имеют общую высоту - их площади относятся как основания.

Поэтому чем больше площадь △ACP, тем больше площадь △ABC.

S(ACP) =1/2 1*1 *sin(ACP)

Чем больше sin(ACP), тем больше площадь △ACP

От 0° до 90° синус возрастает.

∠ACP < ∠ACB < 90° (по условию)

Тогда максимальная площадь △ABC будет при максимально допустимом по условию ∠ACB, 89,(9)°.

Приложения:

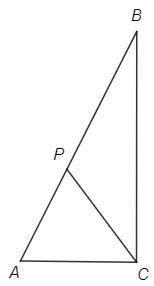
4585o7k5099: я не понимаю где вы нашли общую высоту

4585o7k5099: АСВ не является прямым, только очень сильно приближенным к нему, а АС=РС значит РС не равен 90 градусам

4585o7k5099: это меня и путает, вроде и легко, а вроде сложновато

siestarjoki: Треугольники ACP и ABC имеют общую высоту из вершины С к прямой AB.

4585o7k5099: Недавно вышло решение..., и там ответ: остроугольного треугольника с максимальной площадью не существует....и дальше доказательства..

siestarjoki: Не существует конкретного значения. Но можно указать приблизительное значение с некоторой точностью. Угол стремится к 90, площадь - к максимальной.

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Алгебра, автор: barikmixru

Материальная точка движется прямолинейно по закону x(t)=1/2t^4-2t^3+2t^2+5t+30 , где х - расстояние от точки отсчета в метрах , t - время в секундах , измеренное с начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=1 c

2 года назад

Предмет: Литература, автор: egorgmrr

Капитанская дочка .
Каким образом к семнадцати годам Петрушка , не служа нигде , уже имел офицерский чин ? Почему он рассчитывал служить в Питербурге или в Москве ?

2 года назад

Предмет: Экономика, автор: sambo1s

Декларируется вывозимый из Российской Федерации товар: кожа из шкур крупного рогатого
скота. Объём поставки 9 тыс. кг. Таможенная стоимость товара 31 р. за кг. Ставка пошлины 10 %, но не менее 90 Евро за 1000 кг. Определить сумму таможенной пошлины и таможенные сборы за оформление товара.

2 года назад