Предмет: Математика, автор: schoolpupil

Помогите пожалуйста!!

Приложения:

pushpull: первисна - это производная или первообразна? всё время путаю....

schoolpupil: Производная

pushpull: это не производная, это первообразная...

pushpull: это не производная, а первообразная.... ((((

Ответы

Автор ответа: pushpull

Ответ:

Пошаговое объяснение:

$\displaystyle \int\limits^4_0 {4x} \, dx =4*\frac{x^2}{2} \bigg \vert_0^4=2*4^2-2*0^2=32$

10. y = (x-1)(x+2) = x² +x -2

найдем первообразную

$\displaystyle \int {(x^2+x -2)} \, dx = \frac{x^3}{3} +\frac{x^2}{2} -2x +C$

теперь мы знаем, что точки пересечения графика функции

y = (x-1)(x+2) (1;0) и (-2;0)

через одну из этих точек должен пройти график первообразной

возьмем точку (-2; 0) получим уравнение и из него найдем С

$\displaystyle \frac{(-2)^3}{3} +\frac{(-2)^2}{2} -2*(-2)+C=0; \quad \Rightarrow C=-\frac{10}{3}$

тогда уравнение первообразной будет

$\displaystyle y = \frac{x^3}{3} +\frac{x^2}{2} -2x -\frac{10}{3}$

точки пересечения этих графиков

$\displaystyle \frac{x^3}{3} +\frac{x^2}{2} -2x -\frac{10}{3}=x^2+x-2; \quad \Rightarrow 2x^3-3x^2-18x-8=0$

теперь, зная один корень этого уравнения (х = -2) разложим на множители и получим остальные корни

(х+2)(х-4)(2х+1)=0

тогда сумма абсцисс -2 +4 -0,5 = 1,5

11.

$\displaystyle \int {(3x-1)} \, dx = \frac{3x^2}{2} -x+C$

теперь ищем С по условию

$\displaystyle \frac{3x^2}{2} -x+C=5;$

3x² -2x -2C-10=0

D = b² - 4ac = 4 -4*3(2C-10)

и по условию D = 0

4 -4*3(2C-10) = 0; ⇒ C = 31/6

уравнение первообразной

$\displaystyle y= \frac{3x^2}{2} -x+\frac{31}{6}$

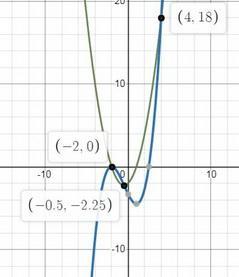
для № 10 графики прилагаются

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Химия, автор: 17044

20 г натрия сожгли полученный оксид вступил в реацию с 19.6 г серной кислоты определите массу соли

2 года назад

Предмет: Алгебра, автор: аня3

Срочнооооооооооооо с решением

2 года назад

Предмет: Физика, автор: AlvySid

В однородной среде распространяется плоская волна с частотой 100 Гц и фазовой скоростью 340 м/с. Найти кратчайшее расстояние между двумя точками среды,
колебания которых происходят в противофазе.