Предмет: Алгебра, автор: Sanya2306

Найти производные (если что, похідна=производная). Разбил на 4 части, чтоб за каждую дать по максимуму баллов. Это 3

Приложения:

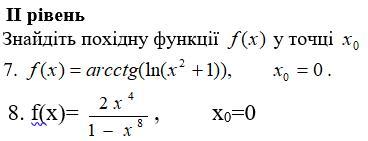
Ответы

Автор ответа: Comentator

Ответ:

f'(arcctgx) = -1/1+x^2

f'(ln(x^2+1)) = 1/(x^2+1)

f'(x^2) = 2x

Формула для 8 примера)f'(u*v) = f'(u)*v-f'(v)*u/v^2

7)f'(0) = -1/1+x^2*1/x^2+1*2x = 2x/(x^2+1)^2 = 2*0/(0^2+1)^2 = 0

8)f'(0) = 2*4x^3*(1-x^8) + 8*x^7*2x^4/(1-x^8)^2 = 8x^3-8x^11+16x^11/(1-x^8)^2 = 0

Объяснение:

Автор ответа: Miroslava227

Ответ:

$f(x) = arcctg( ln(( {x}^{2} + 1))$

$f'(x) = - \frac{1}{1 + {ln}^{2} ( {x}^{2} + 1) } \times ( ln( {x}^{2} + 1))' \times ( {x}^{2} + 1)' = \\ = - \frac{1}{1 + {ln}^{2} ( {x}^{2} + 1)} \times \frac{1}{ {x}^{2} + 1} \times 2x = \\ = - \frac{2x}{( {x}^{2} + 1)(1 + {ln}^{2} ( {x}^{2} + 1)) }$

$f'(0) = 0$

$f(x) = \frac{2 {x}^{4} }{1 - {x}^{8} } \\$

$f'(x) = \frac{( 2{x}^{4})'(1 - {x}^{8}) - (1 - {x}^{8} ) '\times 2 {x}^{4} }{ {(1 - {x}^{8} )}^{2} } = \\ = \frac{8 {x}^{3} (1 - {x}^{8}) + 8 {x}^{7} \times 2{x}^{4} }{ {(1 - {x}^{8} )}^{2} } = \\ = \frac{8 {x}^{3} - 8 {x}^{11} + 16 {x}^{11} }{ {(1 - {x}^{8} )}^{2} } = \frac{8{x}^{3} + 8 {x}^{11} }{ {(1 - {x}^{8}) }^{2} }$