Предмет: Математика, автор: Аноним

СРОЧНО!!!!!!!!!!!!!​

Приложения:

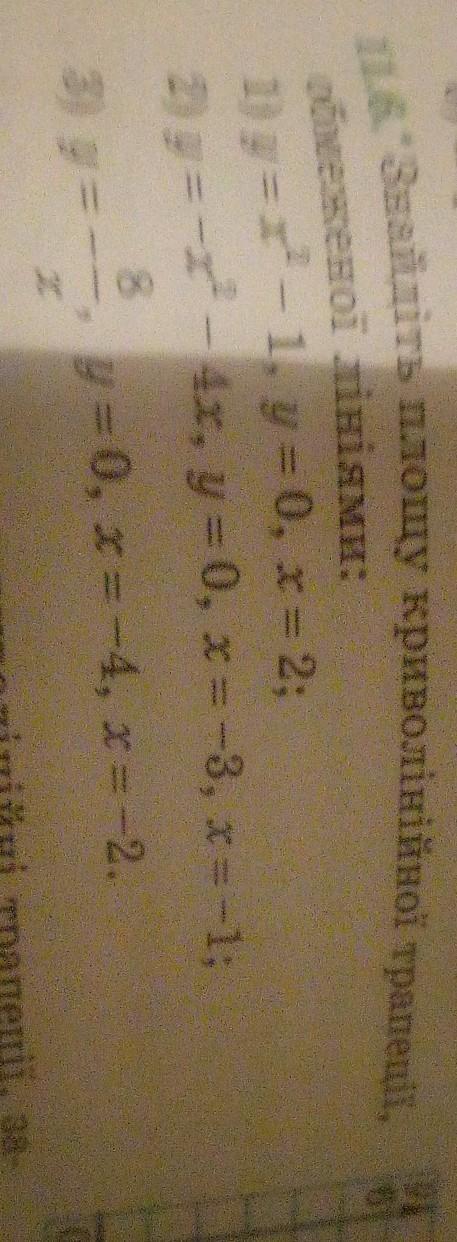
Ответы

Автор ответа: pushpull
1

Ответ:

Пошаговое объяснение:

для каждого пункта рисуем графики и оттуда берем все нужные данные для интеграла

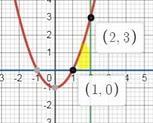
1) y₁ = x²-1;   y₂ = 0;  x = 2

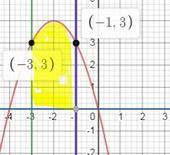
\displaystyle S = \int\limits^2_1 {(x^2-1)} \, dx =\frac{x^3}{3} \bigg \vert_1^2-x \bigg \vert_1^2=\frac{7}{3} -1 =\frac{4}{3}

2) y₁ = -x²-4x; y₂=0; x = -3; x = -1

\displaystyle S=\int\limits^{-1}_{-3} {(x^2-4x)} \, dx =-\frac{x^3}{3} \bigg \vert ^{-1}_{-3}-4\frac{x^2}{2} \bigg \vert ^{-1}_{-3}=-\frac{26}{3} +16=\frac{22}{3}

3)  y₁ = -8/x; y₂=0; x=-4;  x= -2

\displaystyle S=\int\limits^{-2}_{-4} {-\frac{8}{x} } \, dx =-8 \bigg \vert ^{-2}_{-4}= -8 \bigg (ln(-2) - ln(-4) \bigg ) = ln(256)

Приложения:
pushpull: пожалуйста. успехов -)))
Автор ответа: olgaua64
1

Відповідь:

Покрокове пояснення:

∫_a^b інтеграл на інтервалі від а до b

1. S=∫_1^2 (x^2-1)dx=1/3 x^3 - x |_1^2 = 1/3 ×8-2-1/3×1+1 = 7/3-1 = 4/3 = 1 1/3

2. ∫_(-3)^(-1) (-х^2-4х)dx = - 1/3 x^3 - 2x^2 |_(-3)^(-1) = 9 -18 -1/3+2= -7-1/3= -7 1/3

3. ∫_(-4)^(-2) (-8/x)dx= 8 ln(-x) |_(-4)^(-2)= 8(ln 4 - ln 2) = 8× ln(4/2) = 8ln2 = ln 256

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Физика, автор: shonovarman94
Маятник совершает колебания амплитудой 10 мм и частотой 2 Гц. Какова максимальная скорость маятника
2 года назад
Предмет: История, автор: bazarnaya0931
Что из названного стало одной из важнейших задач федеральной власти в России в начале XXI в.?

1)
образование новых субъектов федерации

2)
создание системы судебной власти

3)
подготовка новой редакции Конституции РФ

4)
приведение регионального законодательства в соответствие с общероссийским
2 года назад
Предмет: Экономика, автор: Riko18
Инвестиции в проект Х; составили 5 млн. р., проект рассчитан на 4 года. Чистый денежный поток в месяц составляет в среднем 200 500 руб.,...
Ставка дисконт 0,1 % в месяц определить среднюю норму рентабельности, чистый приведенный доход, сделать вывод о выгодности проекта, индекс прибыльности определив размер прибыли на 1 рубль инвестиций, внутреннюю норму рентабельности, Сформулировать общий вывод
2 года назад
Предмет: Математика, автор: Эви3101
Найди неизвестное число. Выполни проверку. 250- пустое окно=120, пустое окно+350=760. Помогите пожалуйста)
8 лет назад
Предмет: Обществознание, автор: кака154
почему неравенство доходов населения это плохо?
8 лет назад