Из точки D, которая лежит вне плоскости α, проведены к этой плоскости наклонные DK и DB, образующие с ней углы 45° и 60° соответственно. Найдите длину проекции наклонной DK на плоскость α, если DB = 10 корней из 3​

Ответ:

15 ед.

Объяснение:

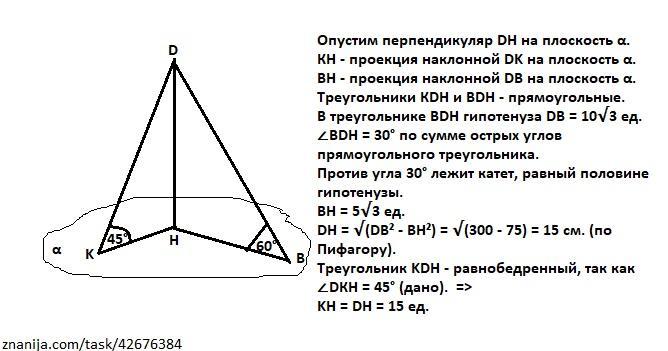
Опустим перпендикуляр DH на плоскость α.

КН - проекция наклонной DK на плоскость α.

ВН - проекция наклонной DВ на плоскость α.

Треугольники КDH и BDH - прямоугольные.

В треугольнике BDH гипотенуза DB = 10√3 ед.

∠BDH = 30° по сумме острых углов прямоугольного треугольника.

Против угла 30° лежит катет, равный половине гипотенузы.

ВН = 5√3 ед.

DH = √(DB² - BH²) = √(300 - 75) = 15 см. (по Пифагору).

Треугольник KDH - равнобедренный, так как  

∠DКH = 45° (дано).  =>  

KH = DH = 15 ед.