Срочно!! даю 50 балов
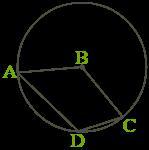
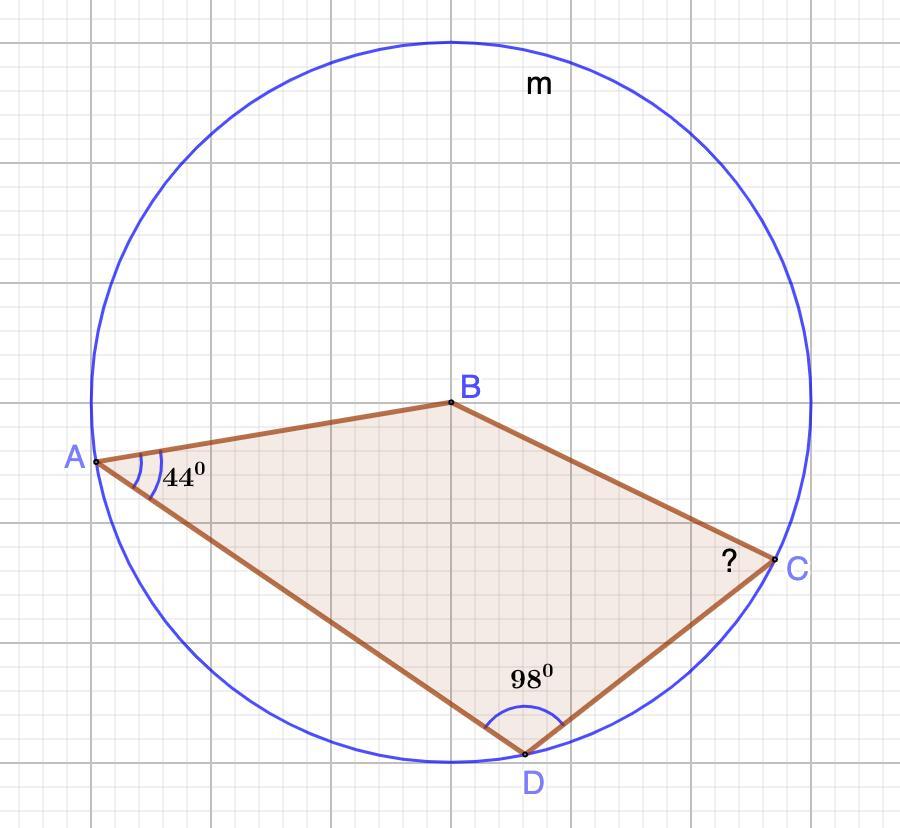
Дан четырёхугольник, три точки которого лежат на окружности, а четвёртая — в её центре. Отрезки, соединяющие эти точки, образуют следующие углы: ∠ADC=98°, ∠DAB=44°. Найди ∠BCD, ответ дай в градусах (запиши только число).

Ответ:

54°

Объяснение:

Дано: Окр.В

ABCD - четырехугольник.

∠ADC = 98°;   ∠DAB=44°

Найти: ∠BCD

Решение:

∠ADC - вписанный.

• Вписанный угол измеряется половиной дуги, на которую он опирается.

⇒ ∪ АmС = ∠ADC * 2 = 98° * 2 = 196°

∪ ADC = 360° - ∪ AmC = 360° - 196° = 164°

∠ ABC - центральный.

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АВС = 164°

• Сумма углов четырехугольника равна 360°.

⇒ ∠BCD = 360° - (∠DAB + ∠ABC + ∠ADC) = 360° - (44° + 164° + 98°)=

=360° - 306° = 54°