Предмет: Математика,
автор: neroun29
помогите решить интеграл
Приложения:
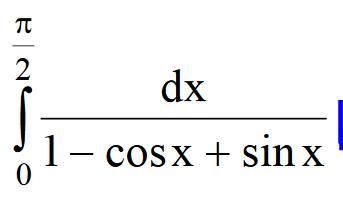
Ответы
Автор ответа:
1
Ответ:
замена:
neroun29:
вы лим забыли добавить
Интересные вопросы
Предмет: Русский язык,
автор: пума4
Предмет: Українська мова,
автор: bellatrix868
Предмет: Қазақ тiлi,
автор: oleg2001748
Предмет: Русский язык,
автор: uljanaantipova
Предмет: Алгебра,
автор: jaylaguseynova