Предмет: Математика, автор: fornes579

Решите уравнение:
sin(2x+2pi/3)*cos(4x+pi/3)-cos(2x)...
Остальное ниже

Приложения:

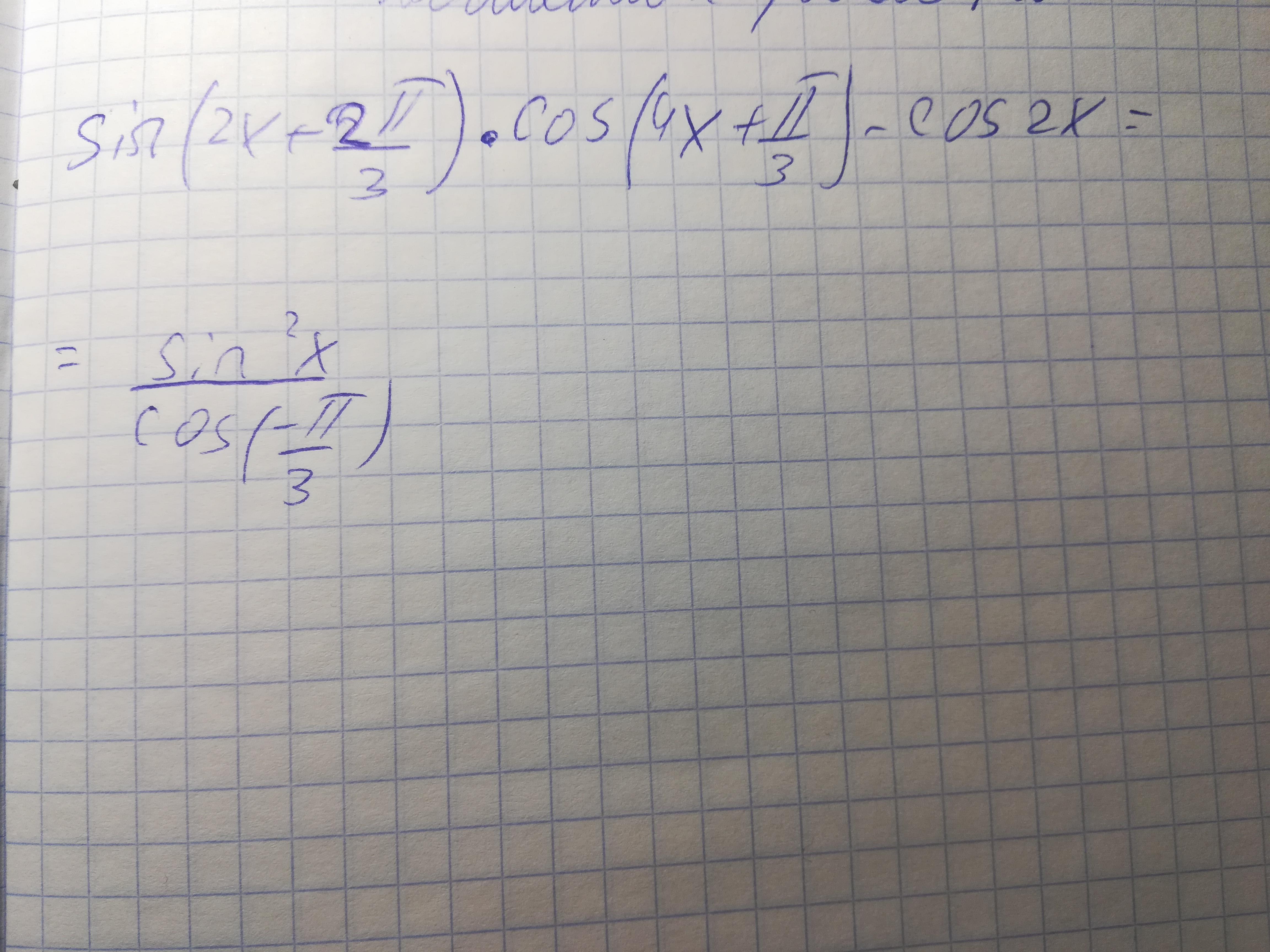
Ответы

Автор ответа: evstifeevzhenya

Ответ:

Ответ: - pi/12 +pin. n € Z

Пошаговое объяснение:Sin(2x+2pi/3)cos(4x+pi/3)-cos2x=sin ^2(x)/cos(-pi/3) ,

Sin(2x+2pi/3)cos(4x+pi/3) = 2 sin ^2(x)+ cos2x,

Sin(2x+2pi/3)*cos(4x+pi/3) = 1

{Sin(2x+2pi/3 )= 1

{cos(4x+pi/3) = 1

{2x+2pi/3= pi/2 +2pin, x = - pi/12 +pin. n € Z

{4x+pi/3=2pin, x= - pi/12 +pin/ 2 = > x = - pi/12 + pin. n € Z

{Sin(2x+2pi/3)= -1

{cos(4x+pi/3)= - 1

{2x+2pi/3= - pi/2 +2pik, x = - 7pi/12+pik,k € Z

{4x+pi/3 = pi +2pik, x= pi/6 +pik/ 2,k € Z = > Ø

armandavtyan1993: Подскажите, пожалуйста, почему не подходят остальные корни? Как проверить, подходит серия корней или нет?

armandavtyan1993: Это-то понятно. Я про другое: Если взять 1-ую систему, имеем серию корней: "-pi/2+pin" и "-pi/12+pi/2" почему в системе подходит именно 1-я серия, хотя на окружности это выглядит вот так:?

armandavtyan1993: К сожалению, не даёт файл прикрепить(

armandavtyan1993: Хотел серию на окружности показать.

armandavtyan1993: Спасибо!