Предмет: Алгебра,
автор: myxocranck
26.9 упростите выражение
Приложения:
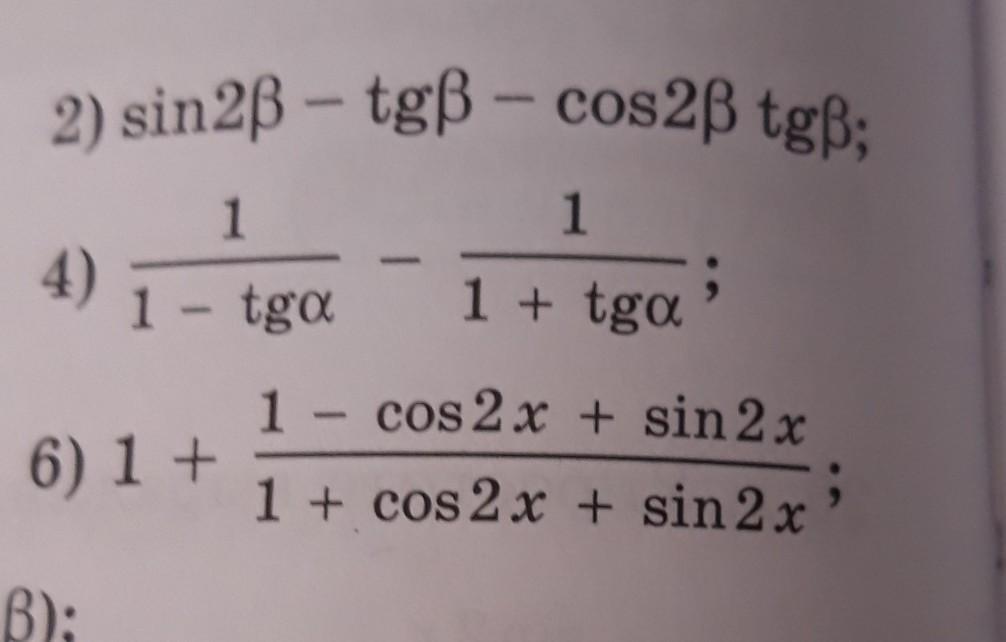
Ответы
Автор ответа:
4
Ответ:
2.
4.
6.
madinabuisobaeva:
извиняюсь но у кого нибудь есть остальное?
Интересные вопросы
Предмет: Русский язык,
автор: sania20031
Предмет: Английский язык,
автор: fesfyra
Предмет: Английский язык,
автор: балерина2
Предмет: Биология,
автор: угвлчлпш
Предмет: Математика,
автор: аниметян3