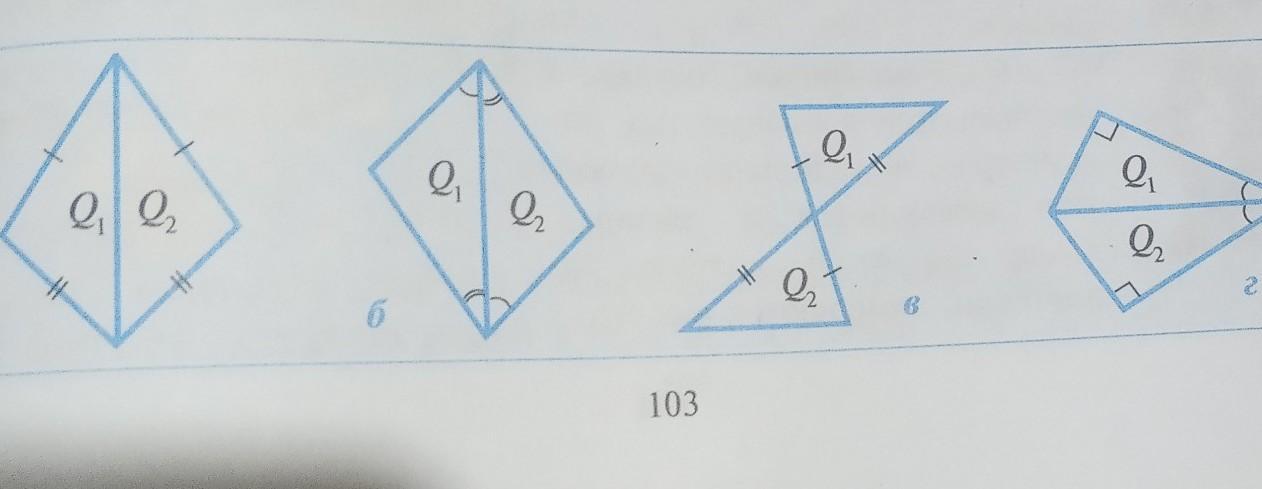
докажите, что треугольники

Q1 и Q2 на рисунке 4 равны!!!​

Ответ: ΔQ₁ = ΔQ₂ по гипотенузе и острому углу.

Объяснение:

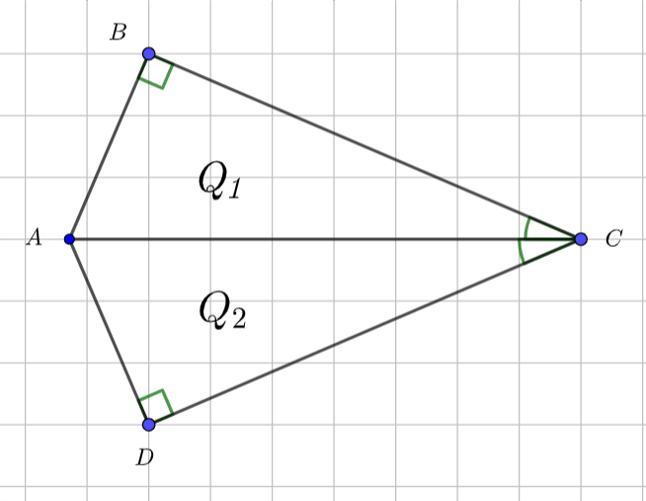
Обозначим верхний треугольник как ABC, нижний — как ADC.

Тогда ∠ABC = 90°; ∠ADC = 90°; ∠BCA = ∠DCA.

Нужно доказать, что ΔABC = ΔADC.

                                   Доказательство:

ΔABC и ΔADC — прямоугольные.

Гипотенуза AC у них общая.

∠BCA = ∠DCA (по условию).

Признак равенства прямоугольных треугольников:

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то эти треугольники равны.

Значит, ΔABC = ΔADC (по гипотенузе и острому углу).