Предмет: Математика, автор: kwartiranowaja

Хочу понять механизм решения, есть идея заменить $\frac{(x-1)}{2}$ на t, но как это делать не очень понимаю, и даже если заменю что делать с уравнением у которого НОД такой страшный

Приложения:

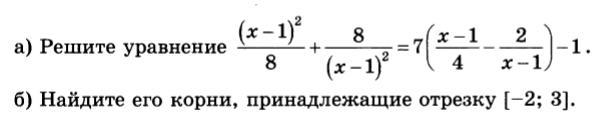
Monemushi: просто скажу, что сначала нужно упросить само уравнение

Monemushi: потом делаешь одинаковые знаменатели в первой части уравнение там где 8 и (x-1)^2. потом и во второй части где 4 и x-1

Monemushi: дальше думаю сам все поймешь и не будет никаких проблем

Monemushi: а решение мне лень писать))

Ответы

Автор ответа: 25hjoerf10

Ответ:

Пошаговое объяснение:

$\frac{\left(x-1\right)^2}{8}+\frac{8}{\left(x-1\right)^2}=7\cdot \left(\frac{x-1}{4}-\frac{2}{x-1}\right)-1\\\\\frac{\left(x-1\right)^2}{8}\cdot \:8\left(x-1\right)^2+\frac{8}{\left(x-1\right)^2}\cdot \:8\left(x-1\right)^2=\frac{7\left(x^2-2x-7\right)}{4\left(x-1\right)}\cdot \:8\left(x-1\right)^2-1\cdot \:8\left(x-1\right)^2\\\\\left(x-1\right)^4+64=14\left(x^2-2x-7\right)\left(x-1\right)-8\left(x-1\right)^2\\\\x^4-4x^3+6x^2-4x+65=14x^3-42x^2-70x+98-8x^2+16x-8$

$x^4-4x^3+6x^2-4x+65=14x^3-50x^2-54x+90\\\\x^4-18x^3+56x^2+50x-25=0\\\\\left(x+1\right)\left(x-5\right)\left(x^2-14x+5\right)=0\\\\1) \: x+1=0\\\\2) \: x-5=0\\\\3) \: x^2-14x+5=0$