Предмет: Математика, автор: SemenSemka

Помогите найти интеграл, внесением функции под знак дифференциала.
Желательно подробно

Приложения:

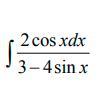
Ответы

Автор ответа: Miroslava227
3

Ответ:

\int\limits \frac{2 \cos(x) }{3 - 4 \sin(x) } dx = - \frac{1}{2} \int\limits \frac{( - 4 \cos(x)) dx}{3 -4 \sin(x) } = \\ = - \frac{1}{2} \int\limits \frac{d(3 -4 \sin(x)) }{ 3 - 4\sin(x) } = - \frac{1}{2} ln(3 - 4 \sin(x) ) + C

SemenSemka: Можете объяснить по-подробнее, как вы про-дифференцировали функцию? Что бы было ясно, почему -1/2 образовалась вообще
Miroslava227: Чтобы решить интеграл способом внесения под знак дифференциала, нужно в числителе сделать производную знаменателя
Miroslava227: (3-4sinx)' = -4cosx
Miroslava227: 2cosx уже дано в числителе
Miroslava227: значит нудно добавить -2
Miroslava227: Приписываем -1/2 * (-2), дробь выходит за знак интеграла, -2 к косинусу
Miroslava227: получили -4cosx и внесли под дифференциал
Miroslava227: интегрируем как переменную
Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: rincolor
Помогите составить диалог. на любую тему 5 класс. не большой))
2 года назад
Предмет: Русский язык, автор: Ледиии
составить предложение со словом храбрый
2 года назад
Предмет: Русский язык, автор: Аноним
Сотавте предложение за схемой [—,(в который...), = и =].
2 года назад
Предмет: Английский язык, автор: Irishaaa2406
Подберите вместо пропусков подходящее по смыслу слово
1. Computers and their ______ equipment are designed by a computer system architect.
a) Engineering; b) accessory; c) specific.
2. Digital computers use numbers instead of analogous physical ______.
a) symbols; b) equipment; c) quantities.
3. Systems ______ are usually stored in read-only memory.
a) hardware; b) software; c) firmware.
4. A computer is a machine with a complex network of electronic ______ that operate switches.
a) circuits; b) cores; c) characters.
5. In modern electronic computers the ______ is the device that acts as a switch.
a) integrated circuit; b) diode; c) transistor.
6. A number of actions that convert data into useful information is defined as______.
a) data; b) processing; c) data processing.
7. Computers can store, organize and retrieve great amounts of information, far beyond the______ of humans.
a) capacities; b) capabilities; c) accuracy.
8. The analyst ______ a computer for solving problems, while the computer system architect ______ computers.
a) requires; b) designs; c) uses.
9. The use of______ computers will continue to increase with the growth in applications of microprocessors and minicomputers.
a) analog; b) digital; c) hybrid.
10. The development of third generation computers became possible due to the invention of______.
a) integrated circuits; b) electronic tubes; c) transistors.
8 лет назад
Предмет: Алгебра, автор: Макс1941м
2 косинус 60 градусов минус 4/5 тангенс 0 градусов плюс 2 синус 45 градусов вычислить
8 лет назад