Предмет: Физика, автор: YakubChim

Автомобиль массой m=1,5 т едет но горизонтальному участку дороги со скоростью v=72 км/ч. На какую величину Delta P увеличивается развиваемая двигателем мощность при движении автомобиля с той же скоростью в гору, угол наклона которой составляет alpha=0,1 рад? Силу сопротивления считать в обоих случаях одинаковой.

Ответы

Автор ответа: mathkot

Ответ:

$\boxed{зP \approx 27 \ 000}$ Вт

Примечание:

$\sin \alpha \approx 0,09$

Объяснение:

Дано:

m = 1500 кг

$v =$ 20 м/c

α = 0,1 рад

g = 10 м/с²

a = 0 м/с²

$F_{T_{1}} = F_{T_{2}}$

Найти:

$зP \ - \ ?$

---------------------------

Решение:

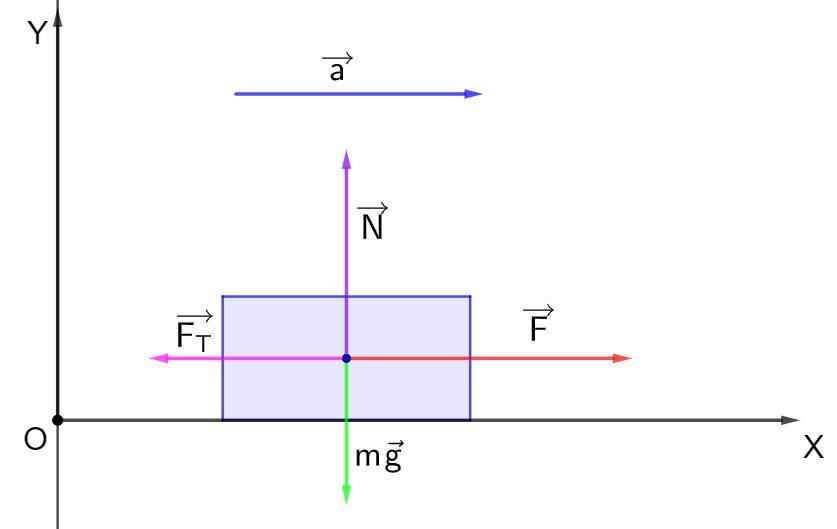
1) Автомобиль на горизонтальном участке пути

$\overrightarrow{F_{T}} + \overrightarrow{F} + \overrightarrow{N} + m \vec{g} = m \vec{a} ;(a = 0)$ - второй закон Ньютона

$OX:F - F_{T} = 0; F = F_{T}$

$OY:N - mg = 0;N = mg$

$F = F_{T} = F_{T_{1}} = \mu N = \mu mg$

$\boxed{F_{T} = F_{T_{1}} = F_{T_{2}} = \mu mg}$

$P_{1} = Fv = \mu mgv;$

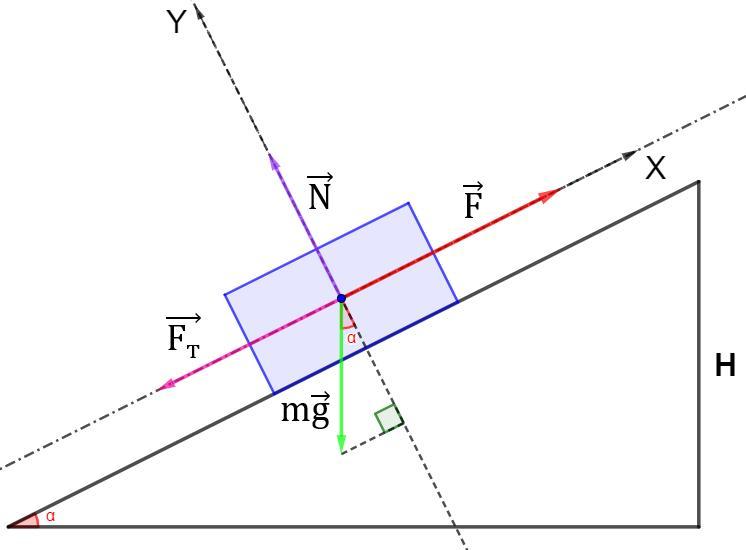
2) Автомобиль на едет под углом

$\overrightarrow{F_{T}} + \overrightarrow{F} + \overrightarrow{N} + m \vec{g} = m \vec{a} ;(a = 0)$ - второй закон Ньютона

$OX:F - F_{T} - mg\sin \alpha = 0; F = F_{T} + mg\sin \alpha;$

$F = F_{T} + mg\sin \alpha = \mu mg + mg\sin \alpha = mg(\mu + \sin \alpha );$

$P_{2} = Fv = mgv(\mu + \sin \alpha );$

$\boxed{зP = P_{2} - P_{1} = mgv(\mu + \sin \alpha ) -\mu mgv = mgv(\mu + \sin \alpha - \mu) =mgv \sin \alpha }$

$зP =$ 1500 кг * 10 м/с² * 20 м/c * 0,09 ≈ 27 000 Вт.

Ответ: $зP \approx 27 \ 000$ Вт.

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: GenerouS1

сочинение по мхк на тему театр

2 года назад

Предмет: Қазақ тiлi, автор: katya232002

36 - жаттыгу. Мына создерди бастауыш етип , моцлемдерди аяктандар.
ауылдын маны- ... .
Балалар шуы - ... .
асык ойнаган ... .
Жыгылган .. .
Алтау ... , торте ... .
Онын айтып отырганы - ... .
Ол ози ... .

2 года назад

Предмет: Окружающий мир, автор: прроро1

рассказ о событии в семье в воскресенье

2 года назад

Предмет: Русский язык, автор: bandreev07

сочинение по картине Игоря Эмануиловича Грабаря "февральская лазурь"

8 лет назад

Предмет: Геометрия, автор: dashafenton

геометрия, 7 класс, признаки параллельности прямых

8 лет назад