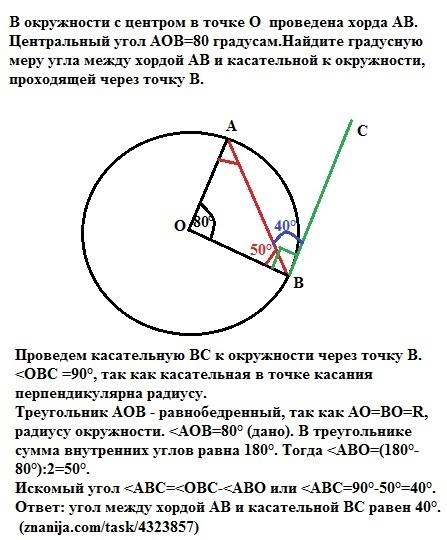
В окружности с центром в точке О  проведена хорда АВ. Центральный угол АОВ=80 градусам.Найдите градусную меру угла между хордой АВ и касательной к окружности, проходящей через точку В.

Проведем касательную ВС к окружности через точку В.
<OBC =90°, так как касательная в точке касания перпендикулярна радиусу.
Треугольник АОВ - равнобедренный, так как АО=ВО=R, радиусу окружности. <AOB=80° (дано). В треугольнике сумма внутренних углов равна 180°. Тогда <ABO=(180°-80°):2=50°.
Искомый угол <АBС=<OВС-<ABO или <AВС=90°-50°=40°.
Ответ: угол между хордой АВ и касательной ВС равен 40°.