Предмет: Математика, автор: vamosmarina6

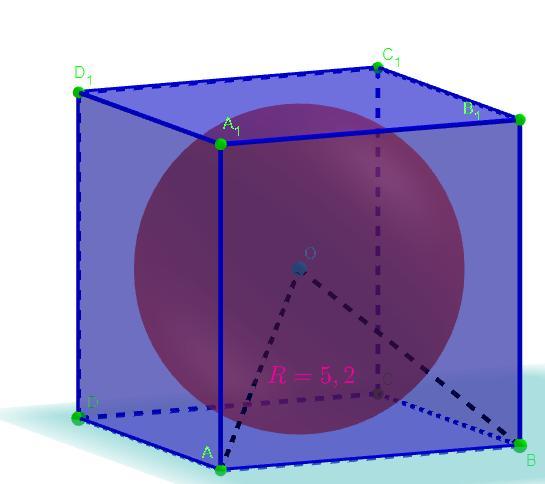
Вычисли объем куба, в который помещен шар, касающийся всех граней куба, с радиусом 5,2 см. Ответ
округли до десятых.

Ответы

Автор ответа: mathkot

Ответ:

$\boxed{V_{kuba} \approx 1124,9}$ см³

Пошаговое объяснение:

Дано: $R = 5,2$ см; шар вписанный в куб; $ABCDA_{1}B_{1}C_{1}D_{1}$ - куб

Найти: $V_{kuba}$ - ?

Решение:

По свойствам шара вписанного в куб его радиус равен половине стороны куба. По свойствам куба все его стороны равны.

$R = \dfrac{AB}{2} \Longrightarrow AB = 2R = 2 \cdot 5,2 = 10,4$ см.

По формуле объема куба:

$V_{kuba} = AB^{3} = 10,4^{3} = 1124,864 \approx 1124,9$ см³.

Приложения:

Интересные вопросы

Предмет: Английский язык, автор: 1234567791

2 года назад

Предмет: Русский язык, автор: андрей240

2 года назад

Предмет: Русский язык, автор: liz12341234

2 года назад

Предмет: Математика, автор: svetakotelniko

8 лет назад

Предмет: Русский язык, автор: Hnduxu478

8 лет назад